| View previous topic :: View next topic |
| Author |
Message |
prcantos
Site Admin
Joined: 17 Apr 2012
Posts: 243
Location: Granada (Spain)



|
 Posted: Feb 20, 2015 10:06 Post subject: Classification of crystallographic forms - any references? Posted: Feb 20, 2015 10:06 Post subject: Classification of crystallographic forms - any references? |
|
|
Hi. I am studying the classification of crystallographic forms. Every systematic book on crystallography describes the 47 or 48 crystallographic forms, but I haven't found any of them that contains the mathematical proof or the foundations of this typology. Why can be said that these are the only forms (of course I consider now the 3D case)? There could be another different ones which are not actually listed?
Please write if you know some references about this theoretic topic. Thank you.
_________________
Pablo Rodríguez Cantos
Λίθον˛ον απεδοκίμασαν˛οι οικοδομουντες |
|
| Back to top |
|
 |
Pete Richards
Site Admin

Joined: 29 Dec 2008
Posts: 828
Location: Northeast Ohio



|
 Posted: Feb 20, 2015 10:50 Post subject: Re: Classification of crystallographic forms - any references? Posted: Feb 20, 2015 10:50 Post subject: Re: Classification of crystallographic forms - any references? |
|
|
Pablo,
I had not heard this limit to the number of forms, but presumably it is secondary to the number of point group symmetries, i.e. crystal classes. It can be shown mathematically that, given the basic elements of translation, rotational axes, mirror planes, and inversion center, there are only 32 possible symmetry classes. For a given crystal class, the symmetry elements operate on a randomly oriented plane to produce symmetrically equivalent planes, the intersection of which is the general crystal form for that symmetry class. In the full symmetry class of the isometric system this is the hexoctahedron. One can then develop special forms by rotating the faces until they coincide pairwise, halving the number of faces. This leads to trapezohedra or trisoctahedra or tetrahexahedra with 24 faces. Further merging leads to the rhombic dodecahedron, the octahedron, and the cube.
There are no other forms given this symmetry. Of course there are an infinite number of possible trapezohedra or trisoctahedra or tetrahexahedra that vary in the angles between the faces.
One can do this exercise for each of the crystal classes and thereby generate all the possible forms. There is still a question of classification of these forms. For example, tetragonal and hexagonal crystals have prisms, in the holohedral case at least there are two prisms and a bi-prism in each class. Does this count as six forms or only one? Pinacoids are found in the triclinic, monoclinic, and some orthorhombic classes. Does each one count separately or is there merely one pinacoid?
Martin Burger's Elementary Crystallography is probably the best treatment of this from a theoretical standpoint that I am aware of. The first 6 chapters treat the symmetry related to external morphology, then the rest of the book gets into crystal structures and their more complex symmetry represented by the space groups.
_________________
Collecting and studying crystals with interesting habits, twinning, and epitaxy |
|
| Back to top |
|
 |
prcantos
Site Admin
Joined: 17 Apr 2012
Posts: 243
Location: Granada (Spain)



|
 Posted: Feb 20, 2015 16:56 Post subject: Re: Classification of crystallographic forms - any references? Posted: Feb 20, 2015 16:56 Post subject: Re: Classification of crystallographic forms - any references? |
|
|
Thank you Peter for this information.
I assume there are 32 three-dimensional point groups. The construction and the proof can be found in 'Mathematical Crystallography: an introduction to the mathematical foundations of crystallography' by M. B. Boisen Jr. & G. V. Gibbs (Mineralogical Society of America 1985 1st. edition, 1990 revised edition) and especially in M. B. Boisen Jr., G. V. Gibbs, 'A derivation of the 32 crystallographic point groups using elementary theory', American Mineralogist (1976) 61, pp. 145-165.
Proved this, you can easily obtain the 32 general forms applying the symmetry operations in these groups on the arbritrary plane (if some of these forms are geometrically identical is a different matter). My problem consists of justifying the 16 special forms.
The method you cited before ('rotating the faces until they coincide pairwise, halving the number of faces') is really interesting, but I think that it isn't systematic or general enough. Furthermore the octahedron can't be obtained by halving the number of faces in the hexoctahedral class: 48, 24, 12 and 6, but never 8.
There is an old article by A. F. Rogers, 'A Tabulation of Crystal Forms and Discussion of Form-Names' (American Mineralogist (1935) 20, pp. 838-851) where another criterion to obtain special forms is given: 'the other 16 forms (48-32=16) are limit forms, the faces of which have a special position whit respect to symmetry directions. These forms are called limit forms since they may be derived from general forms by decreasing certain interfacial angles thus obtaining other general forms until they finally approach the desired form as a limit' (pp. 843-845). This is really a suggestive idea to construct the special forms as limit forms by decreasing interfacial angles, but Rogers doesn't specify it further, he only lists the so-obtained forms. My question is: which are these 'certain' angles? If we consider dihedral angles, it results something similar to that you explained before. Nevertheless to reach the octahedron you need not 'di-hedral' but 'tri-hedral' angles! (just squash a ternary vertex in the thisoctahedron).
But my problem remains because this method isn't systematic or operative enough: 'certain' angles?... Are we sure we have considered all the possible angles? It is rather intuitive, but it lacks generality.
In the memorable third chapter in 'the Dana' a more precise description is stated: a special form 'consists of faces that are parallel or perpendicular to any of the symmetry elements in the crystal class' ('Manual of Mineralogy' by C. Klein and C. S. Hurlbut Jr., 21st edition after J. D. Dana, p. 44). This reference precises the 'special positions' that Rogers had pointed, but anyway a systematic construction of special forms is also absent here. We have again the well-known descriptive list of forms.
D. E. Sands doesn't deal with forms in 'Introduction to Crystallograhpy' (New York 1975), and Boisen & Gibbs only define the forms as 'the collection of equivalent faces' according to the equivalence relation linked to the orbits of the action of the point groups acting on the three-dimensional space (op. cit. pp. 146, 149), but they don't study these orbits.
Most authors seems to assume this typology of forms without worry about its proof.
The book by M. J. Buerger you have cited before is further interesting. I have received this book at home just today, so I haven't studied it yet properly! It contains a noteworthy section titled 'Form theory' (pp. 115-117, 1963 ed.) where you can read a precise formulation of the 'specialized positions' associated with special forms: 'such specialized positions include each of the symmetry elements, positions located between symmetry elements, and the locus on a plane normal to a rotation axis' (p. 117).
This is really a good explanation that explains what was read in Dana ('parallel or perpendicular to any of the symmetry elements'), but I would like to be more precise with those positions 'between symmetry elements'. I suppose than 'between' means 'symmetrically-between' according to the considered symmetry class. Otherwise it lose generallity... Note that the subsequent example in the same page contains the 'symmetry elements', 'the locus on a plane normal to a rotation axis', but not the intermediate positions!
The heart of the matter is, I think, that these mentioned criteria or method to construct special forms or define special positions present a hardly to handle degree of freedom. Some forms show no degree of freedom, I call them 'invariant forms'. They are forms with fixed interfacial angles such the cube {h00}, the dodecahedron {hh0} and the octahedron {hhh} (all the examples in the isometric system). There are also forms that are 'univariant', they can be grouped into families of forms wiht only one degree of freedom. Trisoctahedra {hkk}, trapezohedra {hhk} and tetrahexahedra {hk0} (examples in the hexoctahedral class) constitute univariant families of forms, and there is only one way to modify interfacial angles on them. The general form {hkl} is always a divariant form. The interfacial angles on it can be modified in two independent ways.
I need to study this last book by Buerger carefully. But anyway my personal approach to the classification of forms deals with an abstract algebraic method using matrices. I promise I tell it soon in search of some help from you. Now it is so difficult for me!
_________________
Pablo Rodríguez Cantos
Λίθον˛ον απεδοκίμασαν˛οι οικοδομουντες |
|
| Back to top |
|
 |
Pete Richards
Site Admin

Joined: 29 Dec 2008
Posts: 828
Location: Northeast Ohio



|
 Posted: Feb 20, 2015 22:16 Post subject: Re: Classification of crystallographic forms - any references? Posted: Feb 20, 2015 22:16 Post subject: Re: Classification of crystallographic forms - any references? |
|
|
Hello Pablo,
Thanks for your thorough reply. Perhaps we should be doing this as a private message exchange, but because it started out in public, and there might be some others who can learn from or join in the discussion, I will keep it public for now.
Your thinking is obviously way more advanced than I anticipated in my response; remembering other posts from you, I am not surprised. I will try to reply to the points of your message to which I can add something more.
You said that my method of envisioning moving faces towards each other pairwise until they merged could not produce an octahedron, and you are right. One needs to move three or 3n faces towards each other to reach an octahedron. I sometimes think of general forms like hexoctahedra as being octahedral (or cubic or dodecahedral) balloons that have been over-inflated, so that their sides bulge out (symmetrically and as planes, of course). My example of moving two faces towards each other is just one way of playing with this balloon. Considering the hexoctahedron to be a bulged octahedron, one can push in on the midpoint of the three-fold region until the six faces there collapse into one face, or one can push on the bulge at the four-fold axis until the eight faces surrounding it collapse into one face of a cube. And one can do this on any edge or corner, while requiring that this very dynamic crystal obey your actions by doing so all around the crystal!
There are some very interesting properties of the Miller index representation of faces that can make this quantitative (if not always realistic crystallographically). In particular, the index of a face can be considered a "weighting factor" pulling faces surrounding it toward it. Suppose that we want to make a hexoctahedron (531) into an octahedron (111). If we add the two indices together, we get (642) which equals (321). A crystal drawing will show that this hexoct is flatter in the direction of the three-fold axis than the precursor. Keep doing this, and we wind up with (543), (987), (22.21.20), (101.100.99) etc. with many intermediates. These last are, except for miniscule amounts, equal to (111), and could never occur on actual crystals, except as the mysterious "viscinal faces". One can do the same with moving a hexoct to a cube or a dodec or any other face. This continuum of geometrically possible forms does not exist as a crystallographic continuum, but it does describe the connectedness and relatedness of all forms.
I was not aware of the Rogers paper, but I think you are right that he is saying essentially the same thing that I am. And this notion cannot be confined to dihedral movements. But if you "squash a ternary vertex" as you put it, the dihedral angles around the vertex will all decrease. When they get to 0, you have your octahedron.
Then you discuss some other references including Buerger, and are still not completely satisfied, and you discuss your three-fold classification of forms relative to their degrees of freedom. I agree entirely with your description. Invariant forms (100, 110, and 111 in the isometric system) cannot change in shape, though their shapes may be different in different symmetry classes of the isometric system (e.g. (111) can be an octahedron or a tetrahedron). Univariate forms, though I have not thought of that term before, either have one axis invariant: (hk0), or have two equal axes: (hhk) or (hkk), with h<k (the first case being the trapezohedron and the second being the trisoctahedron). You can change the values of h and k, but you cannot change the basic connection that either one index=0 or two of the indices are equal. And the for remains basically the same. These are still special cases, and lead to a reduced number of faces. (hkl) can occupy all of the geometric space between these special cases, and in fact includes them as special cases.
Now, to some extent explicitly and to some extent implicitly, we have been talking about the holohedral isometric symmetry class. I think everything I/we have said is general, but I have not tried to think it through for a really low-symmetry system such as monoclinic 2. I think probably as you approach this minimal-order state, the general form loses complexity and there are fewer (one?) special forms, and, well, the whole thing just gets less interesting!
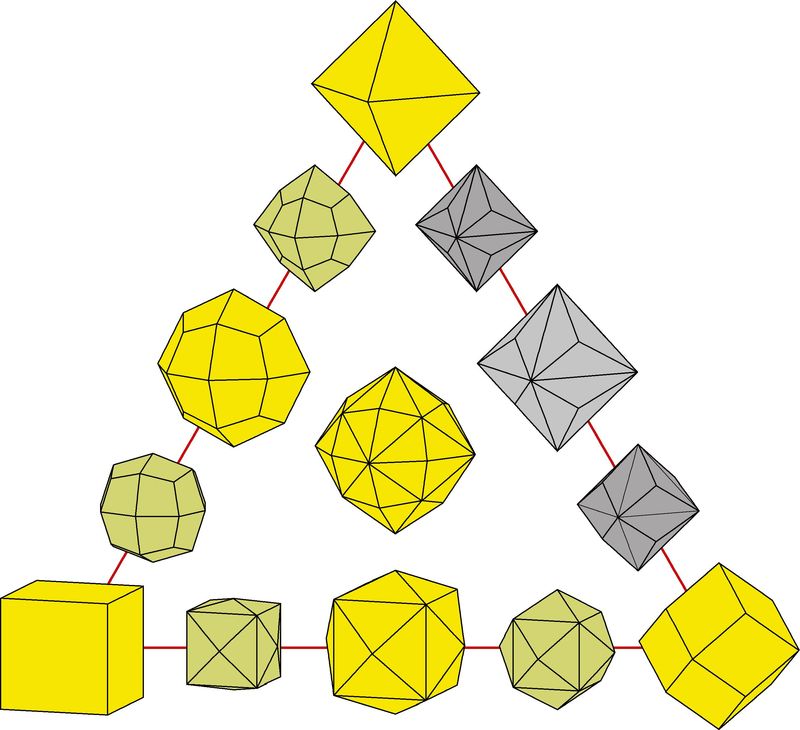
I am attaching a figure I prepared for an article on gold morphology. Ignore the colors of the crystals which were designed for a different purpose. But the poles of the triangle are the invariant forms. Along each axis are forms with one degree of freedom. In the rest of the space the hexoctahedron with two degrees of freedom wanders at will, until it bumps into one of the edges or vertices of the triangle, in which case it becomes "special" and finds its wandering more confined!
| Description: |
| A schematic diagram relating the various form types within the holohedral isometric crystal class. |
|
| Viewed: |
43536 Time(s) |
|
_________________
Collecting and studying crystals with interesting habits, twinning, and epitaxy |
|
| Back to top |
|
 |
Mark Holtkamp
Joined: 26 Dec 2013
Posts: 17


|
 Posted: Feb 21, 2015 05:54 Post subject: Re: Classification of crystallographic forms - any references? Posted: Feb 21, 2015 05:54 Post subject: Re: Classification of crystallographic forms - any references? |
|
|
Hi Pablo,
So if I understand correctly you are looking for a way to mathematically derive the 48 forms, or at least prove there are exactly 48 (or 47)
My mathematics are not good enough to do either. But I have a feeling, for a general solution, it would suffice to look at symmetry operations and single faces only.
The degrees of freedom approach is interesting but I would not look at interfacial angles, because to describe a form, you only need the symmetry operations and a single face (not two faces). I would look at the degrees of freedom of the face normal, i.e. in how many independant directions (if that is the correct term) it can change while leaving the form 'unchanged' (whatever that may mean).
In this way the cube, rhombic dodecahedron and octahedron have no degree of freedom (any change of direction of the face normal would produce another form). The hexoctahedron would have 3 degrees of freedom because rotating the face normal in the x-y, x-z, and y-z plane would not lead to another form (x, y, z being the axes in a 3D coordinate system). The tetrahexahedron has one degree of freedom etc.
Another way perhaps is to look at what happens when using symmetry operations to generate equivalent faces of a form from a single face.
Just some thoughts:
A symmetry center for instance will always generate two faces, (hkl) and (-h-k-l). Both faces make up a pinacoid which is a general form. The symmetry center has no limit or special forms, because there is no h,k,l for which (hkl) equals (-h-k-l) (except 0,0,0 of course).
So if all symmetry operations within a point group, applied to a single face, result in a total number of faces that is less than the maximum number (for the general form) this generated set of faces is a special form. A threefold axis in the cubic system, applied to a face (hkl), will generate (klh) and (lhk), three faces in total. If you have a face for which any of these three generated faces are equal (i.e. willl give less than 3 unique faces), you have found a special form. (111) will leave you with a single face, the cube (100) gives (001) and (010) and is not a special form for the 3-fold axis (but would be for one of the 4-fould axis).
In the holohedral cubic class there are 48 possible faces (all the permutations of h,k,l). Is there a way to derive which, and how many, sets of 48 faces for specific values of h, k and l, have less than 48 unique faces?
Mark
|
|
| Back to top |
|
 |
prcantos
Site Admin
Joined: 17 Apr 2012
Posts: 243
Location: Granada (Spain)



|
 Posted: Feb 21, 2015 08:08 Post subject: Re: Classification of crystallographic forms - any references? Posted: Feb 21, 2015 08:08 Post subject: Re: Classification of crystallographic forms - any references? |
|
|
| Pete Richards wrote: | | ...Perhaps we should be doing this as a private message exchange, but because it started out in public, and there might be some others who can learn from or join in the discussion, I will keep it public for now... |
Yes, please!! ;-) Thank you Peter and Mark. I think I will study your posts this evening, they contain much interesting information. Meanwhile I provide you the link to the paper by Rogers. It is free available in the Mineralogical Society of America website:
https://www.minsocam.org/ammin/AM20/AM20_838.pdf
_________________
Pablo Rodríguez Cantos
Λίθον˛ον απεδοκίμασαν˛οι οικοδομουντες |
|
| Back to top |
|
 |
Mark Holtkamp
Joined: 26 Dec 2013
Posts: 17


|
 Posted: Feb 22, 2015 08:57 Post subject: Re: Classification of crystallographic forms - any references? Posted: Feb 22, 2015 08:57 Post subject: Re: Classification of crystallographic forms - any references? |
|
|
Paul Tambuyser in his book 'Kristalmorfologie' (in Dutch) uses an interesting method to systematically derive all crystal forms. I don't know if this method is used by other authors. It is based on dividing a spherical projection of a crystal class in 'elementary triangles' and use these as an aid in determining possible forms. In every triangle in the projection there are 7 possible positions (and therefore 7 crystallographic forms): 3 positions on the corners of the triangle; these positions have no degrees of freedom. 3 positions on the edges of the triangle, with one degree of freedom. The 7th position has 2 degrees of freedom and represents the general form. Apparently in this method there is no need for something like 'positions between symmetry elements'.
In the cubic system these positions match with Miller indices {100}, {110}, {111}, {hk0}, {hhl}, {hkk} and {hkl}. These are the well-known cubic forms. In the triclinic system, for instance,{100}, {010}, {001}, {0kl}, {h0l}, {hk0} and {hkl}, which all are pinacoids in the holoedric class (the a-pinacoid, b-pinacoid etcetera). With 32 point groups, this leads to 7 x 32 different crystal forms (ignoring correlate forms).
Some of these 7*32 forms are geometrically equivalent (e.g. all pinacoids, all tetragonal prisms etc.) and by grouping those together I guess 47 (or 48) basic forms remain.
Mark
|
|
| Back to top |
|
 |
Pete Richards
Site Admin

Joined: 29 Dec 2008
Posts: 828
Location: Northeast Ohio



|
 Posted: Feb 22, 2015 12:32 Post subject: Re: Classification of crystallographic forms - any references? Posted: Feb 22, 2015 12:32 Post subject: Re: Classification of crystallographic forms - any references? |
|
|
| Mark Holtkamp wrote: | Paul Tambuyser in his book 'Kristalmorfologie' (in Dutch) uses an interesting method to systematically derive all crystal forms. I don't know if this method is used by other authors. It is based on dividing a spherical projection of a crystal class in 'elementary triangles' and use these as an aid in determining possible forms. In every triangle in the projection there are 7 possible positions (and therefore 7 crystallographic forms): 3 positions on the corners of the triangle; these positions have no degrees of freedom. 3 positions on the edges of the triangle, with one degree of freedom. The 7th position has 2 degrees of freedom and represents the general form.
(snip)
Mark |
This is exactly what my diagram above shows for the holohedral isometric class, though I did not place (100), (110), and (111) in the positions they would occupy in a spherical projection, but just made them the vertices of an equilateral triangle.
_________________
Collecting and studying crystals with interesting habits, twinning, and epitaxy |
|
| Back to top |
|
 |
Mark Holtkamp
Joined: 26 Dec 2013
Posts: 17


|
 Posted: Feb 22, 2015 16:30 Post subject: Re: Classification of crystallographic forms - any references? Posted: Feb 22, 2015 16:30 Post subject: Re: Classification of crystallographic forms - any references? |
|
|
Hi Pete,
Yes you're right. it's the same principle. I didn't realise this can be done for all pointgroups.
Mark.
|
|
| Back to top |
|
 |
Pete Richards
Site Admin

Joined: 29 Dec 2008
Posts: 828
Location: Northeast Ohio



|
 Posted: Feb 22, 2015 16:50 Post subject: Re: Classification of crystallographic forms - any references? Posted: Feb 22, 2015 16:50 Post subject: Re: Classification of crystallographic forms - any references? |
|
|
| Mark Holtkamp wrote: | Hi Pete,
Yes you're right. it's the same principle. I didn't realise this can be done for all pointgroups.
Mark. |
I'm not sure what the apices of the triangle would be for triclinic bar-1. No particular reason to choose (110) and (111) since they are not special forms. Would Tambuyser use (100), (010), and (001), since they each only intersect one axis? Even so, they still belong to pinacoids.
Or what about monoclinic 2 or monoclinic m, where there's only one axis of symmetry or one axis that is perpendicular to a mirror plane? Of course you still have three axes... with well-defined angles between them: 90, beta, and 90. I guess the lattice still has 2/m symmetry, even though the morphology and the structure do not.
I prefer crystals with high symmetry!
_________________
Collecting and studying crystals with interesting habits, twinning, and epitaxy |
|
| Back to top |
|
 |
Mark Holtkamp
Joined: 26 Dec 2013
Posts: 17


|
 Posted: Feb 23, 2015 16:31 Post subject: Re: Classification of crystallographic forms - any references? Posted: Feb 23, 2015 16:31 Post subject: Re: Classification of crystallographic forms - any references? |
|
|
| Yes that is what he does. The projections of the holohedral classes are divided in triangles by the symmetry planes. So you have 48 triangles in the cubic system, but none in the monoclinic and triclinic system. Here, the apices of the triangles are the unit cell axes. Hence the listing of a- b- and c-pinacoid, the h0l pinacoid etc. This list seems a bit arbitrary since as you said all forms are pinacoids.
|
|
| Back to top |
|
 |
prcantos
Site Admin
Joined: 17 Apr 2012
Posts: 243
Location: Granada (Spain)



|
 Posted: Feb 24, 2015 17:37 Post subject: Re: Classification of crystallographic forms - any references? Posted: Feb 24, 2015 17:37 Post subject: Re: Classification of crystallographic forms - any references? |
|
|
I have been studying some different methods to construct and distinguish all the possible forms. You have already mentioned them here, but I would like to do some comments.
The first method involves what Peter described before as 'a dynamic crystal'. This is the idea from Rogers' article: decreasing certain interfacial angles up to both faces collapse. This method was very suggestive to me, but it don't stand in many cases.
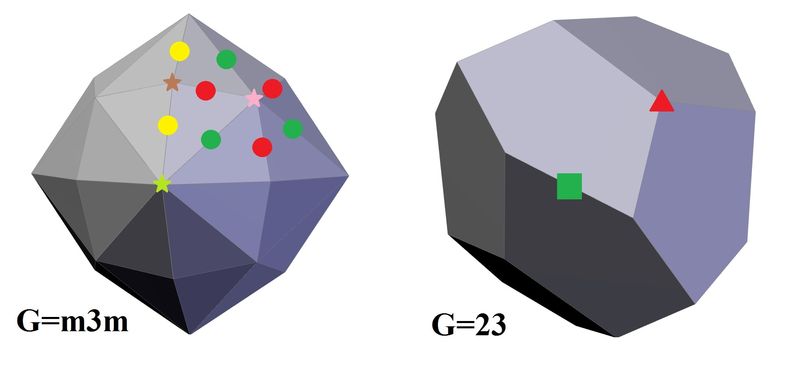
For example let's consider hexoctahedron (general form for the group G=m3m). You can easily squash different edges or vertices and obtain the six remaining special or limit forms (see the first picture). But are you sure you have covering all the possibilities? Now try to do the same with groups with less symmetry level (try it with G=-43m or G=23): this is more difficult. And furthermore notice that some special forms has the same number of faces than the general form, so you can't get them by decreasing angles or collapsing faces! Example for G=23: the general form (tertartoid) has twelve faces, the same as the special forms deltoid-dodecahedron, tristhetrahedron, pyritohedron and dodecahedron.
The second method concerns some special positions respect to the symmetry elements. This is the idea we find in Dana, Buerger, Klockmann-Ramdohr, Tambuyser... and it usually uses the stereographic projection to represent tridimensional objects on the paper. This is a very clear graphic method. The symmetry elements provide a net of axes and planes which are represented by points and lines in the stereogram. This net divides the circle into several curved triangles (projection of spherical triangles). It is not difficult to prove that the three corners of each triangle match invariant forms, the three edges match univariant forms, and the inner area match the general form (which is divariant, not trivariant).
But this method has two important lacks:
1) It depends essentially on a particular graphic representation, which is not desirable. What about if you change the representation system? Is the classification different? Pete has proposed a different way to arrange the forms in an equilateral triangle: how does it work now? Recently I also designed a triangular representation similar to that we use to study igneous rocks and metamorphic parageneses. And many more could be conceived...
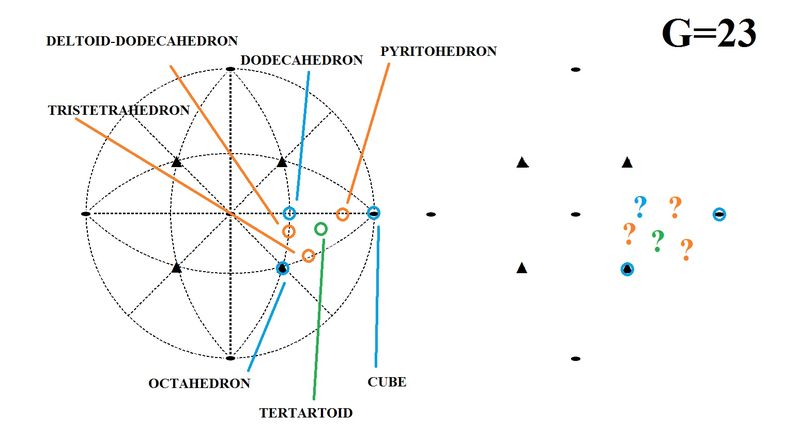
2) There are many groups where the stereogram is usually drawn using dashed discontinuous lines. These broken lines represent some symmetry elements that don't fit the group. They can be useful as a reference system, but you shouldn't use them to classify the forms: if a plane is not a plane of symmetry now, why do you use its projection to delimit the triangles you use for the classification? In the second picture I have drawn on the left the stereogram for G=m3m (hexoctahedral class), where dashed lines show the symmetry elements of G=m3m, the upper-level symmetry group in the isometric system, as it appears in every book of Crystallography. On the right I put the same stereogram drawing only the elements that appear in fact (four 3-fold axes, marked with triangles, and tree 2-fold axes, marked by ellipses). How do you recognize the special positions without these dashed-references?
These remarks lead me to think that maybe the classification of the crystallographic forms is not proved enough, or I haven't found the complete proof yet. As a mathematician, I would like to have a completely abstract method to do this classification, something similar to classical algebraic or geometric topics such the classification of quadratic forms o the isometries... I have done several attempts and they seem to work properly in some simple cases (for example when the point group is cyclic), but definitely they fail whit polyaxial groups. In a next post I will show you some examples of this algebraic approach and explain some troubles I find.
| Description: |
| The method suggested by Rogers. On the left the hexoctahedron can be squashed in some different ways to get the special forms for G=m3m. Press it on the red points and you will get the trisoctahedron; press the green points and get the trapezohedron; the yellow dots for the tetrahexahedron; press the brown star and get the dodecahedron; the pink star for the octahedron; and the green star for the cube. But now try it again with the tertartoid on the right (G=23). You will only get a cube (green square) and a octahedron (red triangle). What about the rest of the special forms? |
|
| Viewed: |
42913 Time(s) |
|
| Description: |
| Dashed discontinuous lines for symmetry elements that don't stand for the considered group. You should draw it whitout references, but how will you place the forms then? |
|
| Viewed: |
42910 Time(s) |
|
_________________
Pablo Rodríguez Cantos
Λίθον˛ον απεδοκίμασαν˛οι οικοδομουντες |
|
| Back to top |
|
 |
Pete Richards
Site Admin

Joined: 29 Dec 2008
Posts: 828
Location: Northeast Ohio



|
 Posted: Feb 25, 2015 10:25 Post subject: Re: Classification of crystallographic forms - any references? Posted: Feb 25, 2015 10:25 Post subject: Re: Classification of crystallographic forms - any references? |
|
|
Pablo is right that that my method of "pushing on edges (or vertices)" to collapse the general form to special forms is not universally applicable. I find it appealing where it does work because it emphasizes the continuously variable nature non-fixed forms (at least if one ignores the Law of Simple Rational Indices). This is a geometric concept, not particularly a crystallographic one, since crystals do tend to obey this "Law".
I'm NOT a mathematician, but it is intuitive to me that there is no difference between my triangular representation of forms and one like in Pablo's message, unless perhaps one wants to do computations of specific forms occupying particular places on the triangle. I.e. they are qualitatively the same. This seems to be analogous to maps that use different projections to depict the globe. They distort the sphere in various ways to make it flat. Any of the maps can get you from point A to point B, but some are better than others, for example, in the polar latitudes, and some are not very good at telling you how to travel in an airplane, where you can take any path you want, but generally want the shortest path.
There is quite a good discussion of the 48 forms starting on page 114 of the Buerger book I introduced some time ago. I am happy for the discussions in this thread of ours, because I have had that book for a long time but never explored it very thoroughly.
Finally, while it is a little off topic, I attach for your interest a stereographic projection of all of the 700 or so forms of calcite contained in a famous list compiled by Charles Palache. It is interesting to note how strongly forms are concentrated in specific zones, and how some regions of the projection are crystallographic deserts!
| Description: |
| Stereographic projection of the forms of calcite. Each dot represents one face of a recognized form. |
|
| Viewed: |
43026 Time(s) |

|
_________________
Collecting and studying crystals with interesting habits, twinning, and epitaxy |
|
| Back to top |
|
 |
prcantos
Site Admin
Joined: 17 Apr 2012
Posts: 243
Location: Granada (Spain)



|
 Posted: Feb 25, 2015 11:04 Post subject: Re: Classification of crystallographic forms - any references? Posted: Feb 25, 2015 11:04 Post subject: Re: Classification of crystallographic forms - any references? |
|
|
| Pete Richards wrote: | | ...I'm NOT a mathematician, but it is intuitive to me that there is no difference between my triangular representation of forms and one like in Pablo's message, unless perhaps one wants to do computations of specific forms occupying particular places on the triangle. I.e. they are qualitatively the same. This seems to be analogous to maps that use different projections to depict the globe. They distort the sphere in various ways to make it flat... |
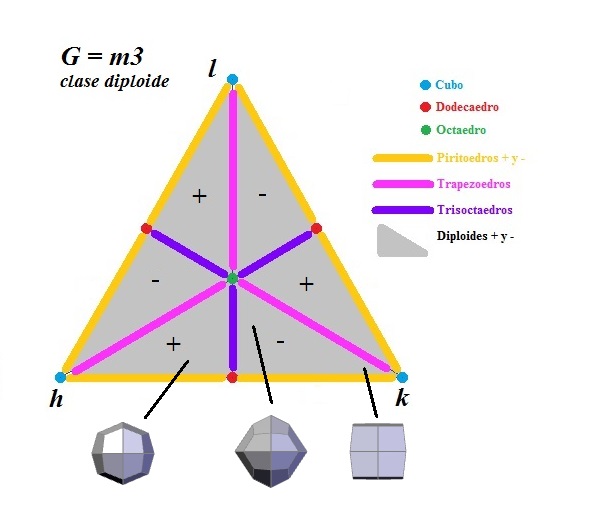
Well, in algebraic terms we have chosen two different 'bases' or 'systems of reference': in your triangle you have {100}, {110} and {111} in the corners, and I have {100}, {010} y {001}. They both are possible and right.
I haven't introduced my triangular representation yet. I am doing it now in the picture. But my problem with any of them is the same: why must draw some 'inner lines' connecting forms? If those lines match symmetry elements, it is so clear (e. g. G=m3m). But what about another groups which lack some of those elements? Why does everybody keep the lines?
| Description: |
| {hkl}-triangular representation of the forms in the diploidal class. Names are in Spanish, but they are really similar to them in English. Vertex "h" matches the form {100} because h=1, k=0 and l=0. Vertex "k" matches {010} and "l" {001}. I have drawn some examples of positive and negative diploids. You can easily see why these forms are classified as 'invariant' (represented by single points), 'univariant' (represented by segments or lines with dim=1, you can move along the line and modify the aspect of the form) and 'divariants' (represented by areas, with dim=2, you can move with 2 degrees of freedom along the plane). |
|
| Viewed: |
42863 Time(s) |
|
_________________
Pablo Rodríguez Cantos
Λίθον˛ον απεδοκίμασαν˛οι οικοδομουντες |
|
| Back to top |
|
 |
prcantos
Site Admin
Joined: 17 Apr 2012
Posts: 243
Location: Granada (Spain)



|
 Posted: Feb 25, 2015 11:29 Post subject: Re: Classification of crystallographic forms - any references? Posted: Feb 25, 2015 11:29 Post subject: Re: Classification of crystallographic forms - any references? |
|
|
Erratum!!! In picture 'dudaStPrj.jpg' where is written 'OCTAHEDRON' it should appear 'TETRAHEDRON' of course! I do apologize.
_________________
Pablo Rodríguez Cantos
Λίθον˛ον απεδοκίμασαν˛οι οικοδομουντες |
|
| Back to top |
|
 |
prcantos
Site Admin
Joined: 17 Apr 2012
Posts: 243
Location: Granada (Spain)



|
 Posted: Feb 26, 2015 16:35 Post subject: Re: Classification of crystallographic forms - using matrices Posted: Feb 26, 2015 16:35 Post subject: Re: Classification of crystallographic forms - using matrices |
|
|
| prcantos wrote: | | ...I will show you some examples of this algebraic approach and explain some troubles I find. |
Now I am going to show my attempt to classify the forms using matrices. The method consists of two stages:
Stage A) You have to construct a matrix which resumes the symmetry of the point group in certain sense. This is the inventive part.
Stage B) You have to study that matrix using an accurate matricial method. This is the technical part.
Here you have a very easy example involving a low-symmetry group G=4 (tetragonal-pyramidal class).
G=4 is a cyclic group generated by the 4-fold rotation around [001] axis. Let ρ be that symmetry operation. Thus G={1,ρ,ρ^2,ρ^3}, where 1 is the identity operation. If B_0 is the usual orthonormal basis of R^3, the matrix for ρ is the matrix M in the first picture.
Stage A) Let us construct a 3x3 squared matrix A that resumes the symmetry of G. Let (h,k,l) be an arbitrary vector in R^3 (you can pick it on the unit sphere as well). Using M we calculate ρ(h,k,l) and ρ^2(h,k,l). These resultant vectors will be the second and the third column of A. The first column will be 1(h,k,l)=(h,k,l). The columns of the matrix A contain the essential information of the action of G applied to the arbitrary vector (h,k,l).
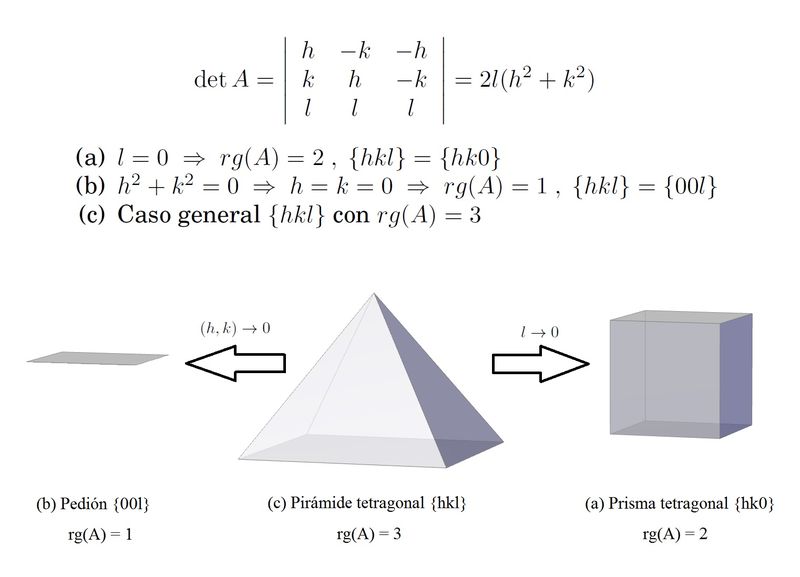
Stage B) This matrix is supposed to be useful to classify the forms for G. In this simple case we can discuss the rank of A (2nd picture) solving the equation det A = 0. We obtain the three possible forms matched to the three possible values for the rank. The general form is the tetragonal pyramid (rank 3), and two special forms: the tetragonal prism (rank 2) and the pedion (rank 1).
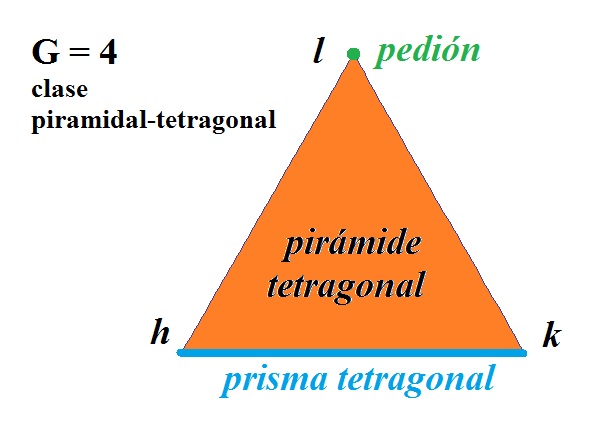
Finally we can represent this result in the {hkl}-diagram (3rd picture).
| Description: |
| Preparing the matrix A... |
|
| Viewed: |
42645 Time(s) |
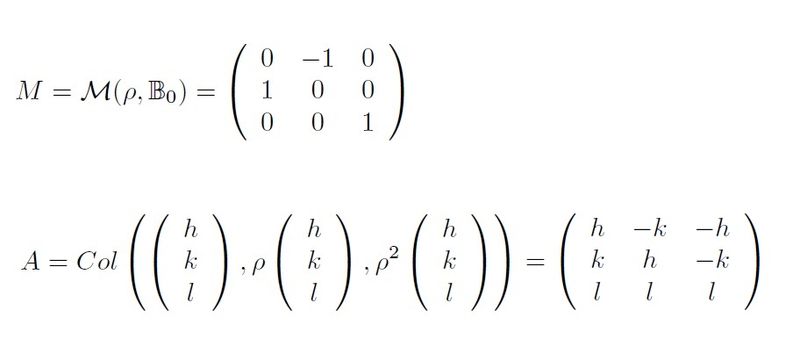
|
| Description: |
| Discussing the ranks and identifying the resultant forms... |
|
| Viewed: |
42679 Time(s) |
|
| Description: |
| Showing the results in the {hkl}-triangle... |
|
| Viewed: |
42757 Time(s) |
|
_________________
Pablo Rodríguez Cantos
Λίθον˛ον απεδοκίμασαν˛οι οικοδομουντες |
|
| Back to top |
|
 |
Roger Warin
Joined: 23 Jan 2013
Posts: 1175



|
 Posted: Feb 26, 2015 17:13 Post subject: Re: Classification of crystallographic forms - any references? Posted: Feb 26, 2015 17:13 Post subject: Re: Classification of crystallographic forms - any references? |
|
|
Hi Pete
Thank you for sharing this concept. I had not thought to consider in this respect the distribution of all forms of calcite. I am even surprised with the results.
I think this projection deserves a new topic with comments about this new milky way. Many thanks.
Roger.
|
|
| Back to top |
|
 |
Pete Richards
Site Admin

Joined: 29 Dec 2008
Posts: 828
Location: Northeast Ohio



|
 Posted: Feb 26, 2015 17:23 Post subject: Re: Classification of crystallographic forms - any references? Posted: Feb 26, 2015 17:23 Post subject: Re: Classification of crystallographic forms - any references? |
|
|
Thanks Roger,
I agree this could be a whole new direction in these discussions, and I could add more. I do not know how to branch a thread - perhaps our chief guru Jordi can do this. I'll be glad to participate!
_________________
Collecting and studying crystals with interesting habits, twinning, and epitaxy |
|
| Back to top |
|
 |
prcantos
Site Admin
Joined: 17 Apr 2012
Posts: 243
Location: Granada (Spain)



|
 Posted: Feb 27, 2015 05:07 Post subject: Re: Classification of crystallographic forms - any references? Posted: Feb 27, 2015 05:07 Post subject: Re: Classification of crystallographic forms - any references? |
|
|
Peter, perhaps you could start a new thread for the calcite forms topic. Or maybe you prefer to write a 'theoretic approach' in this outstanding thread containing many pictures:
Calcite Forms - (4).
Both would be a really interesting topic!
Please let me make just some remark or question about calcite 'forms'. The word 'form' in Crystallography means 'a set of equivalent faces' according to symmetry relations. Thus calcite can only show these 6 forms, the only possible for G=-32/m (Hexagonal Scalenohedral class): pinacoid, hexagonal prism, rhombohedron, hexagonal dypiramid, hexagonal scalenohedron and dihexagonal prism (cf. 'Dana' op. cit. p 91, table after Buerger op. cit.).
The rest of 'global configurations' of faces in crystals should be called with a different term I think, but not 'form'. Do you think so?
_________________
Pablo Rodríguez Cantos
Λίθον˛ον απεδοκίμασαν˛οι οικοδομουντες |
|
| Back to top |
|
 |
Pete Richards
Site Admin

Joined: 29 Dec 2008
Posts: 828
Location: Northeast Ohio



|
 Posted: Feb 27, 2015 10:13 Post subject: Re: Classification of crystallographic forms - any references? Posted: Feb 27, 2015 10:13 Post subject: Re: Classification of crystallographic forms - any references? |
|
|
| prcantos wrote: |
Please let me make just some remark or question about calcite 'forms'. The word 'form' in Crystallography means 'a set of equivalent faces' according to symmetry relations. Thus calcite can only show these 6 forms, the only possible for G=-32/m (Hexagonal Scalenohedral class): pinacoid, hexagonal prism, rhombohedron, hexagonal dypiramid, hexagonal scalenohedron and dihexagonal prism (cf. 'Dana' op. cit. p 91, table after Buerger op. cit.).
The rest of 'global configurations' of faces in crystals should be called with a different term I think, but not 'form'. Do you think so? |
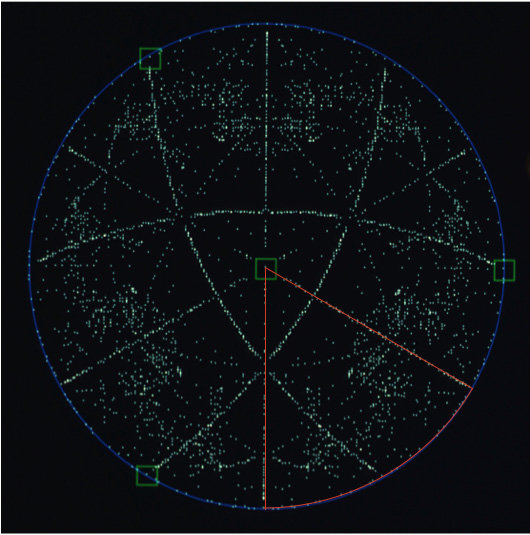
Pablo, you are right. What my stereographic projection really shows is the the poles in the upper hemisphere of the faces of all known forms of calcite. So dihexagonal prisms are represented by 12 dots (all along the bounding circle), scalenohedra, prisms, and hexagonal dipyramids are represented by 6 dots, rhombohedra by 3, and the pinacoid by 1.
The region representing the forms, if it is assumed that the forms have their usual indices (e.g. (21-31) and not the equivalent (-3211), is the region bordered by red in this modified diagram.
I think showing the whole hemisphere is more interesting and more pleasing, because it really depicts the symmetry as it acts to replicate faces.
| Description: |
|
| Viewed: |
42620 Time(s) |
|
_________________
Collecting and studying crystals with interesting habits, twinning, and epitaxy |
|
| Back to top |
|
 |
|


