| View previous topic :: View next topic |
| Author |
Message |
Ru Smith
Joined: 13 Oct 2012
Posts: 362



|
 Posted: May 27, 2013 10:16 Post subject: Re: About cyclic twinning - (5) Posted: May 27, 2013 10:16 Post subject: Re: About cyclic twinning - (5) |
|
|
| Yes, excellent detective work.
|
|
| Back to top |
|
 |
Peter Farquhar
Site Admin

Joined: 14 May 2011
Posts: 52
Location: Virginia



|
 Posted: Jun 24, 2013 09:02 Post subject: Re: About cyclic twinning - (5) Posted: Jun 24, 2013 09:02 Post subject: Re: About cyclic twinning - (5) |
|
|
The Spanish Forum has a new thread on Maclas ("Twinning") that is superb. Pep Gorgas started the thread, and it has grown significantly with original explanations to some of the difficult questions posed in this thread. Pablo Rodriguez Cantos has added new mathematical analyses of twinning that has stimulated much discussion with its insights.
With Google Translate, this thread can be read in almost any language. For anyone interested in learning more about cyclic twinning, I highly recommend you visit https://www.foro-minerales.com/forum/viewtopic.php?t=9242
In the meantime, I'm working on posting more on this thread soon.
Peter Farquhar
|
|
| Back to top |
|
 |
Peter Farquhar
Site Admin

Joined: 14 May 2011
Posts: 52
Location: Virginia



|
 Posted: Jul 23, 2013 16:46 Post subject: Re: About cyclic twinning - (5) Posted: Jul 23, 2013 16:46 Post subject: Re: About cyclic twinning - (5) |
|
|
Identical twins
On this thread in August 2012, I posted a photographic plate from Louis Pope Gratacap’s famous 1912 book, “A Popular Guide to Minerals.” The 1907 plate showed three Parkesburg, Pennsylvania rutile twins from the Clarence S. Bement collection in the American Museum of Natural History in New York City. The exquisite rutile specimen in the center of this plate is a complete sixling (see below).
In April 2013, I posted Peter Cristofono’s 2012 photo of a Parkesburg, Pennsylvania rutile sixling in the Harvard Mineralogical Museum collection (#110229) in Cambridge, Massachusetts. This rutile is a great specimen to see in person.
Below is a side-by-side comparison of the Parkesburg rutile specimens from Gratacap’s 1907 black and white photo and Cristofono’s 2012 color photo. I was surprised to discover that Harvard’s rutile is indeed the same Bement specimen depicted in Gratacap’s book. The two twinned specimens are identical!
Peter Farquhar
Claremont, California
USA
| Description: |
Rutiles
Parkesburg, Chester County, Pennsylvania USA
L.P. Gratacap photo of three Clarence S. Bement rutile specimens from the American Museum of Natural History in New York City (1907) |
|
| Viewed: |
46431 Time(s) |

|
| Description: |
Rutile
Parkesburg, Chester County, Pennsylvania USA
4 cm
Comparison of the same cyclic twinned rutile specimen (Harvard-110229) as photographed in 1907 vs. 2012.
Color photo by Peter Cristofono is copyrighted 2012 and used with his permission. |
|
| Viewed: |
46487 Time(s) |

|
|
|
| Back to top |
|
 |
Peter Farquhar
Site Admin

Joined: 14 May 2011
Posts: 52
Location: Virginia



|
 Posted: Sep 03, 2013 18:11 Post subject: Re: About cyclic twinning - (5) Posted: Sep 03, 2013 18:11 Post subject: Re: About cyclic twinning - (5) |
|
|
Many collectors are familiar with the distinctive rutile sixlings labeled from Parkesburg, Pennsylvania. These cyclic twinned rutile specimens were usually found in loose soil along a 30-mile valley that stretches far beyond Parkesburg: from the plowed fields east of Pomeroy; along the railroad cut and roadway running to the west; across several small farms in Sadsbury, Parkesburg, Atglen, Christiana, and other towns; and then southwest to the farm fields of Constitution, Pennsylvania and across the border into nearby Maryland.
Nevertheless, almost identical rutile sixlings are found at a few other localities, too. I would like to share some of these specimens in this thread on cyclic twinning.
For example, the cyclic twinned rutile (PF-3191) pictured below is a complete sixling from Inyanga, Rhodesia -- now called Nyanga in the Nyanga District, Manicaland Province, Zimbabwe. While rutile has been reported from several locations in Zimbabwe (mostly as rutile sands or thin-needles in quartz), these are the first published photographs I’ve seen of a Zimbabwe rutile specimen.
There is no history of mining activity in the Nyanga District, which is in the eastern highlands of Zimbabwe bordering Mozambique. For centuries, the small communities around Nyanga village lived in relative isolation and focused on agriculture, livestock, and architecture. Mineral specimens from this region are understandably scarce. Because of the nearby mountains, waterfalls, and national parks, Nyanga has become a small center for tourists visiting northeastern Zimbabwe in the past few years.
One might guess that years ago a farmer found this rutile sixling while working the terraced fields to the north of the village of Nyanga. Indeed, a satellite close-up view of the farm fields around Nyanga looks surprisingly similar to the fields around Parkesburg today. One might also wonder how many more rutile specimens are lying in these northeastern Zimbabwe farm fields, like the old “money stones” found in Pennsylvania farm fields from the mid-1800s to present.
Peter Farquhar
Claremont, California
USA
| Description: |
Rutile sixling (PF-3191) - front
Inyanga, Rhodesia (now Nyanga, Nyanga District, Manicaland Province, Zimbabwe.
2.5 x 2.3 x 1.8 cm
A complete rutile sixling from a surprising locality -- the farm fields north of Nyanga village in Zimbabwe. Front side of the specimen. |
|
| Viewed: |
46170 Time(s) |

|
| Description: |
Rutile sixling (PF-3191) - back
Inyanga, Rhodesia (now Nyanga, Nyanga District, Manicaland Province, Zimbabwe
2.5 x 2.3 x 1.8 cm
A complete rutile sixling from a surprising locality -- the farm fields north of Nyanga village in Zimbabwe. Back side of the specimen. |
|
| Viewed: |
46130 Time(s) |

|
|
|
| Back to top |
|
 |
prcantos
Site Admin
Joined: 17 Apr 2012
Posts: 243
Location: Granada (Spain)



|
 Posted: Sep 04, 2013 03:55 Post subject: Re: About cyclic twinning - (5) Posted: Sep 04, 2013 03:55 Post subject: Re: About cyclic twinning - (5) |
|
|
Hi, Peter. Another outstanding rutile!
I would like to ask you why you call it 'a sixling'. The front face of the specimen combines four principal twins according to a cyclic or concentrical description, and some geniculated ones (small vvvvvvv) than can be seen near the center of the group.
The back face appears to be more regular (despite of imperfections) with five main individuals and two little terminations or tails. Could you put another picture showing a side-view of the junction where these two tails get together?
_________________
Pablo Rodríguez Cantos
Λίθον˛ον απεδοκίμασαν˛οι οικοδομουντες |
|
| Back to top |
|
 |
Roger Warin
Joined: 23 Jan 2013
Posts: 1232



|
 Posted: Sep 04, 2013 04:08 Post subject: Re: About cyclic twinning - (5) Posted: Sep 04, 2013 04:08 Post subject: Re: About cyclic twinning - (5) |
|
|
Hi,
I think it is a habit in the Anglo-Saxon literature. Would it not be a lattice of 3 x 2 centered parts?
Roger.
|
|
| Back to top |
|
 |
Peter Farquhar
Site Admin

Joined: 14 May 2011
Posts: 52
Location: Virginia



|
 Posted: Sep 06, 2013 17:43 Post subject: Re: About cyclic twinning - (5) Posted: Sep 06, 2013 17:43 Post subject: Re: About cyclic twinning - (5) |
|
|
| prcantos wrote: | | Hi, Peter. Another outstanding ruitle! I would like to ask you why you call it 'a sixling'. |
In answering your question, I researched the etymology of the term “sixling” and its early uses for cyclic twinned rutiles.
I found most of the early scientific publications on cyclic twinned rutiles were written in German (e.g., the seminal article by noted crystallographer Gustav Rose (1862), “Ueber eine neue kreisformige Verwachsung des Rutils,” Annalen der Physik und Chemie (Poggendorff), vol. 115, pp. 643-649). In the mid-1800s, the German word “sechsling” typically referred to a set of sextuplets, or a coin worth six pfennigs. Professor Rose’s colleagues and students apparently adopted the word “sechsling” as a shorthand for his longer, more descriptive expressions (e.g., “gruppe von sechs kreisformig verbundenen Rutilkrystallen” (a group of six circularly connected rutile crystals). The word “sechsling” soon appeared in Rose’s subsequent scientific publications, and became widely adopted and translated into other languages.
The word “sixling” (after the German) first appeared in English-language publications around 1890. The term initially referred to planar, six-fold cyclic twinned rutiles – similar to Gustav Rose’s 1862 idealized drawing (e.g., see G. H. Williams’ (1890) adaptation below). Later, the word “sixling” was also used to describe the pseudohexahedral dipyramids of rutile paramorphs after brookite from Magnet Cove, Arkansas, USA and elsewhere; I’ll explore these cyclic twins in a separate post.
So the century-old term “sixling” is a shorthand for rutiles, even though it’s an imperfect descriptor. Earlier in this thread (e.g., see his posts on August 20, 2012), Pete Richards explained why the word “sixling” does not accurately describe flat cyclic twinned rutiles: the angle across the twin planes for rutile is 65 degrees, instead of 60 degrees, so there is always a misfit in closing the loop. Nevertheless, planar five-sided rutile twins with one (or more) short “tails” are commonly called “sixlings” (see Pete Richards’ excellent 3-D colored illustration of how “a theoretically accurate rutile sixling” deviates from “an ideal hexagonal outline).”
In colloquial use, planar cyclic twinned rutile specimens with five good sides (plus one or more short "tails") are typically called "complete" sixlings, while those with perhaps three or four sides (plus tails) are called "incomplete" or "partial" slxlings. This practice, however, has led to occasional abuse and some wishful thinking by dealers and collectors.
I hope this explanation helps. Please let me know if you have further information on the origins and meanings of the word “sixling” or its predecessors.
Peter Farquhar
Claremont, California
USA
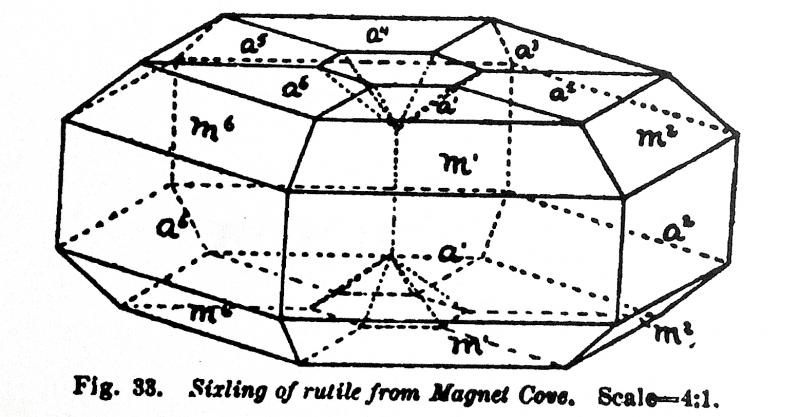
| Description: |
Rutile sixling (idealized drawing)
Graves Mountain, Georgia USA
From G. H. Williams (1890), "Elements of Crystallography," Henry Holt Publishers (New York), p. 198, as reproduced in "Annual Report of the Geological Survey of Arkansas for 1890," vol. 2 (1891), p. 325.
Note Williams' use of the term "sixling." This idealized drawing originally appeared in Professor Rose's 1862 article, and was attributed to Graves Mountain, not Magnet Cove as Williams reported.
Over the past 150 years, countless adaptations of Gustav Rose's idealized drawing have been published in books and articles to illustrate a rutile sixling; e.g., see John White's posting in this thread showing this diagram from figure 40 in John Sinkankas' book "Mineralogy," (1964, p. 99). |
|
| Viewed: |
45930 Time(s) |
|
|
|
| Back to top |
|
 |
GneissWare

Joined: 07 Mar 2008
Posts: 1287
Location: California



|
 Posted: Sep 06, 2013 18:44 Post subject: Re: About cyclic twinning - (5) Posted: Sep 06, 2013 18:44 Post subject: Re: About cyclic twinning - (5) |
|
|
Peter,
Nice bit of history! Thanks!
|
|
| Back to top |
|
 |
prcantos
Site Admin
Joined: 17 Apr 2012
Posts: 243
Location: Granada (Spain)



|
 Posted: Sep 07, 2013 03:25 Post subject: Re: About cyclic twinning - (5) Posted: Sep 07, 2013 03:25 Post subject: Re: About cyclic twinning - (5) |
|
|
Thank you, Peter, for your masterful and well-documented explanation. If I could learn something from Pete Richards' posts, it is that cyclic rutiles hardly ever show exact hexagonal parameters, as you have remarked as well.
Thus my question derives from the lack of a satisfactory Spanish synonym for 'sixling'. When I translated this thread into Spanish FMF I used the construction 'macla séxtuple' (something like 'sixfold twin'), which implies six individuals exactly; 'eightlings' implies eight ones and so on.
Now that we have your explanation I should revise and improve the translation according to this information in some weeks' time.
_________________
Pablo Rodríguez Cantos
Λίθον˛ον απεδοκίμασαν˛οι οικοδομουντες |
|
| Back to top |
|
 |
Peter Farquhar
Site Admin

Joined: 14 May 2011
Posts: 52
Location: Virginia



|
 Posted: Sep 08, 2013 16:19 Post subject: Re: About cyclic twinning - (5) Posted: Sep 08, 2013 16:19 Post subject: Re: About cyclic twinning - (5) |
|
|
| prcantos wrote: | Thus my question derives from the lack of a satisfactory Spanish synonym for 'sixling'. When I translated this thread into Spanish FMF I used the construction 'macla séxtuple' (something like 'sixfold twin'), which implies six individuals exactly; 'eightlings' implies eight ones and so on.
Now that we have your explanation I should revise and improve the translation ... |
I appreciate your question and reply about use of the word “sixling.” It is perhaps easy to forget the impact of different languages in accurately conveying an idea. This may be an opportunity for you to invent a new Spanish word for rutile “sixlings” – which often do not have exactly six sides. At the same time, I welcome your English word “tail” to describe one of more short sides of a rutile sixling that do not fit neatly in the circle. Thanks for a perfect word choice.
Earlier you asked for additional photos of the rutile sixling (PF-3191) from Nyanga, Zimbabwe showing the junction where the two tails come together.
The first view (labeled “bottom-up”) tips the specimen in the earlier “front” view backwards – so the original “front” of the specimen is now on top in this photo, and the original “back” is now on the bottom in this photo. Here you can see where the tails meet.
The second view (labeled “left-side”) is obtained by rotating the “bottom-up” orientation counter-clockwise by 90 degrees. Here you can see a perfect fit with the "non-tail" sides.
I look forward to your further comments and analysis of this unusual cyclic twinned rutile from Nyanga, Zimbabwe.
Peter Farquhar
Claremont, California
USA
| Description: |
Rutile sixling (PF-3191) bottom-up
Inyanga, Rhodesia (now Nyanga, Nyanga District, Manicaland Province, Zimbabwe)
2.5 x 2.3 x 1.8 cm
Bottom view of a complete rutile sixling from the farm fields north of Nyanga village in Zimbabwe. |
|
| Viewed: |
45742 Time(s) |

|
| Description: |
Rutile sixling (PF-3191) left-side
Inyanga, Rhodesia (now Nyanga, Nyanga District, Manicaland Province, Zimbabwe)
2.5 x 2.3 x 1.8 cm
Left-side view of a complete rutile sixling from the farm fields north of Nyanga village in Zimbabwe. |
|
| Viewed: |
45784 Time(s) |

|
|
|
| Back to top |
|
 |
Peter Farquhar
Site Admin

Joined: 14 May 2011
Posts: 52
Location: Virginia



|
 Posted: Oct 26, 2013 19:31 Post subject: Re: About cyclic twinning - (5) Posted: Oct 26, 2013 19:31 Post subject: Re: About cyclic twinning - (5) |
|
|
Several contributors to this thread have explained why cyclic-twinned rutile specimens cannot form closed hexagonal loops with six equal sides. Because of their tetragonal structure, cyclic twinned rutile crystals intersect at an angle of about 114 degrees. Complete rutile “sixlings” therefore usually have only five good sides plus a short tail or two.
But six-sided rutile twins do exist!
The secret to this paradox is pseudomorphism. In particular, rutile can assume the orthorhombic structure of brookite, instead of its characteristic tetragonal crystalline structure. Since rutile and brookite have the same chemical composition (titanium dioxide), this special type of pseudomorph is called a “paramorph.”
[Moderator's correction: The text below has been updated to refer to the rutile sixling twin (PF-2402), whose image is found in a subsequent posting. The images of the rutile paramorph after brookite (PF-1960) were originally posted by mistake.]
The rutile paramorph (PF-2402) has the habit of a pseudo-hexagonal bipyramid. While Magnet Cove eightlings of rutile are familiar, such six-sided rutile specimens are extraordinarily scarce. While these rutile paramorphs are referred to as “sixlings” (e.g., Max Bauer, 1891), additional research may be needed to determine whether they are cyclic “sixlings” formed by six individuals in rotation around a vertical axis, or “trillings” of interpenetrating twins (cf. Pete Richards’ FMF thread, “Twinning of Aragonite”).
Arkansas State Geologist Mike Howard (1999) explains the paramorphic transformation of these rutile specimens. The initial brookite most likely formed at some moderate temperature; as the temperature increased, the paramorphic transformation began to convert the brookite to rutile starting from the exterior surface and then extending inward to the core. In many cases, the temperature was apparently not elevated long enough to complete the transformation entirely to rutile. As a result, the outside faces of some paramorphs are entirely rutile, while the interior core remains brookite. (J. Michael Howard, “Brookite, Rutile Paramorphs after Brookite, and Rutile Twins from Magnet Cove, Arkansas” (Rocks and Minerals, vol. 74, no. 2, March/April 1999, pp. 92-102.))
These rutile paramorph sixlings were found as loose float in a single plowed field on the Richardson Farm in Magnet Cove, Arkansas, from the late 1870s to the 1880s, when the site was exhausted. The Richardson Farm is located in the north-central part of Magnet Cove about 0.8 km east of the eastern entrance to the Magnet Cove Rutile Company deposit along the east-west road that crosses the Richardson property. The field itself is located immediately south of this road, about 120 meters west of the Richardson farm buildings, and just above the north side of Cove Creek. About 80 meters to the southeast of this field are the abandoned shafts of the pyrite mines operated briefly by the Confederacy in the early 1860s.
The few Magnet Cove rutile paramorph sixlings found since the 1880s were discovered either at the Magnet Cove Rutile Company deposit less than 1.0 km to the west of Richardson find, or at the collecting area in Cove Creek adjacent to the Mo-Ti Prospect less than 0.4 km to the east. None of these later discoveries rival the size or quality of the rutile sixlings from the original Richardson find. After fifty years of collecting, Arkansas mineralogist Arthur E. Smith, Jr. (1933-2009) observed that rutile paramorph sixlings are “very rare, and I have never seen any good specimens from Magnet Cove” to compare with those from Richardson Farm depicted in Bauer (1891) and elsewhere. See Art Smith, “Magnet Cove Rutile Sixlings and Eightlings,” in The Backbender’s Gazette, November 2007, pp. 4-8.
The rutile paramorph sixling (PF-2402) below has a distinctive history – it was once part of the Kimzey family mineral collection. Arkansas historical records indicate Fleming W. “Hodge” Kimzey (1850-1890) purchased a “good farm” in 1874 just west of Cove Creek, along the main highway crossing Magnet Cove from east to west. Hodge’s farm was surrounded by Perovskite Hill, Calcite Hill, and other soon-to-be famous mineral localities. William Jennings Kimzey (1851-1906) joined his brother Hodge in Magnet Cove shortly after, and more Kimzey family members followed later. Hodge reportedly “engaged in farming to some extent, and extensively in mineral collecting.” Meanwhile, William J. “engaged in prospecting the area and collecting fine specimens of numerous rare minerals for the leading dealers and some English, French, and German scientists.”
The Kimzey brothers collected this rutile paramorph sixling at the Richardson Farm around 1880; the farm field was just a 2 km walk from their homes heading northeast along Cove Creek. They decided to save this particular specimen for their own collection instead of selling it. Art Smith noted, “Many of the early finds were put in collections that were sent to Germany where there evidently was more of a demand for them” – particularly with prominent German mineralogists like Max Bauer who used these rutile specimens for his research on paramorphism.
After William J. Kimzey’s death in 1906, three of his seven sons continued the family tradition of “seeking out specimens of the unusual and rare minerals” around Magnet Cove. In particular, his son Joseph Wood Kimzey (1888-1975) managed the mineral business and the Kimzey family collection. Joe Kimzey also had a distinguished legal and political career at the Arkansas state and local levels; he served as the Arkansas State Geologist for a time, was quite active in mining development in Magnet Cove, and enthusiastically promoted mineral collecting.
The Kimzey Mineral Collection was listed in guidebooks of Arkansas attractions while it was displayed in a family log cabin in Magnet Cove. The collection was also on public display at the Arkansas state capital for several years. See Richard S. Mitchell, “Joseph Wood Kimzey and Members of the Kimzey Family,” Rocks and Minerals, vol. 62, no. 4, July/August 1987, pp. 252-253.
This exceptional rutile paramorph sixling remained in the Kimzey family mineral collection from around 1880 when it was discovered until 1935, when Joe Kimzey sold it to a well-known American mineral dealer in whose private collection it remained for more than fifty years. It is now one of two prized Magnet Cove sixlings in my rutile collection.
Peter Farquhar
Claremont, California
USA
| Description: |
Rutile paramorph after brookite (PF-1960)
Magnet Cove, Arkansas USA
2.9 x 2.6 x 1.8 cm |
|
| Viewed: |
44416 Time(s) |

|
| Description: |
Rutile paramorph after brookite (PF-1960)
Magnet Cove, Arkansas USA
2.9 x 2.6 x 1.8 cm |
|
| Viewed: |
44393 Time(s) |

|
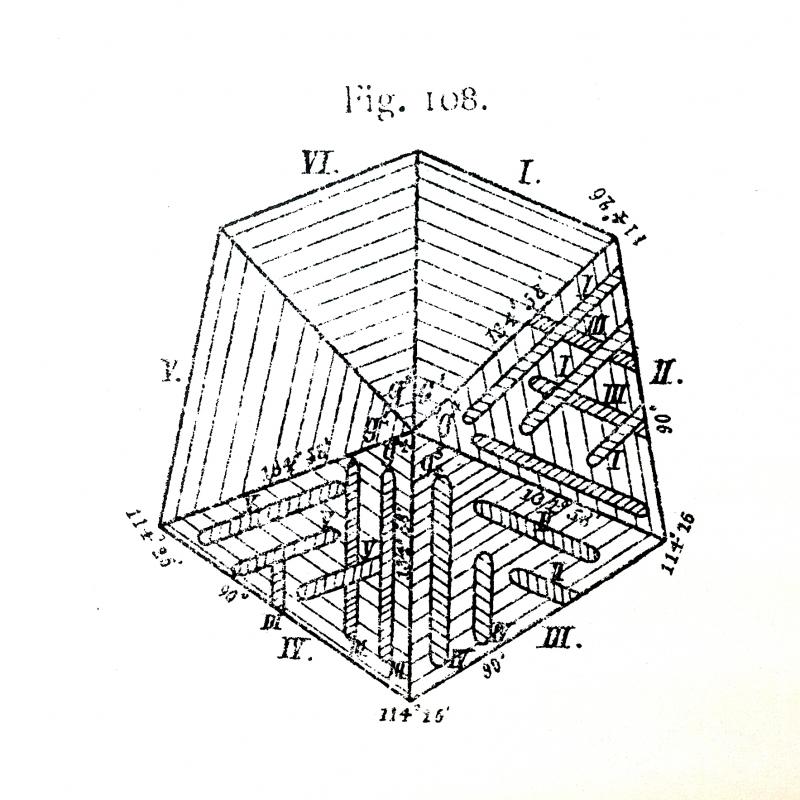
| Description: |
Rutile paramorph sixling (drawing)
Magnet Cove, Arkansas, USA (published 1891)
Sketch of a rutile paramorph after brookite published in 1891 by Max Bauer, "Beitrage zur Mineralagie. VII. Reihe, 14, "Uber die Paramorphosen von Rutil nach Brookit von Magnet Cove, Arkansas." Neues Jahrbuch fur Mineralogie,, Geologie, und Paleontologies, 1, Taf. 5, Fig. 1, as reproduced in 1922 by Victor Goldschmidt in "Atlas der Krystallformen" Vol VII, Taf. 156, Fig. 108.
This sketch depicts one of the rutile paramorphs after brookite that the Kimzey brothers collected at the Richardson Farm and then sent to the German mineralogist Max Bauer in the early 1880s for his research on rutile paramorphism. |
|
| Viewed: |
44393 Time(s) |
|
| Description: |
Ruitle paramorph sixling (drawing)
Magnet Cove, Arkansas USA (published 2007)
Sketch of an idealized rutile sixling from Magnet Cove by Art Smith and published in "Magnet Cove Rutile Sixlings and Eightlings,"The Backbender's Gazette, November 2007, p.7, fig 6. Compare this sketch of a rutile paramorph after brookite with a pseudohexagonal bipyramid habit to the actual specimen shown earlier. |
|
| Viewed: |
44394 Time(s) |

|
|
|
| Back to top |
|
 |
Antonio Alcaide
Site Admin

Joined: 23 Aug 2009
Posts: 314
Location: Spain



|
 Posted: Oct 27, 2013 01:54 Post subject: Re: About cyclic twinning - (5) Posted: Oct 27, 2013 01:54 Post subject: Re: About cyclic twinning - (5) |
|
|
Peter, you never give up surprising us. You have contributed to create an increasing group of rutile lovers here on FMF. Thanks for this new fragment of the rutile history.
Regards
_________________
Life is the shortest crystal |
|
| Back to top |
|
 |
prcantos
Site Admin
Joined: 17 Apr 2012
Posts: 243
Location: Granada (Spain)



|
 Posted: Sep 03, 2015 05:48 Post subject: Re: About cyclic twinning - (5) Posted: Sep 03, 2015 05:48 Post subject: Re: About cyclic twinning - (5) |
|
|
How many twins are there in a cyclic twin?
What would you say? Is a cyclic twin a unique multiple twin, or better a set of several simple twins? Should it be described using a rotation or many reflections?
Friedel's theory about twinning states that in every twin a 'twinning lattice' can be described. This 'twinning lattice' is a periodic lattice that fits the whole set of twinned individuals, and its restriction to any of the individuals is a sublattice. This twinning lattice is typical of true twins, but can't be described in arbitrary crystalline aggregates.
According to the periodicity of this twinning lattice, the 'Crystallographic Restriction Theorem' (see C. Klein & C. S. Hurlbut Jr. [after J. D. Dana], Manual of Mineralogy, 21st ed., p. 115-116) runs and states that the only possible values for a n-fold axis in a crystalline lattice are n = 2, 3, 4 & 6. Notice that the only hypothesis in this theorem is the periodicity of the lattice, which stands in a twinning lattice.
As a consequence we have that a cyclic twin, where a rotation axis can be easily recognized, can be considered as 'one multiple twin' only in case it shows a 2, 3, 4 or 6-fold axis. Otherwise it must be described as a set of several reflection twins according to several mirrors so that the mirror planes intersect all at the axis, but never as a unique multiple twin.
Example: rutile sixlings
Rutile sixlings are cyclic twins formed by several individuals around a rotation axis with a 65º angle (see https://www.mineral-forum.com/message-board/viewtopic.php?p=25309#25309 ). If it were a 60º angle, we would have a 6-fold axis and could call it a true [multiple] twin. But as the angle is 65º the associated axis is a 72-fold axis, which is impossible for a single periodic lattice, and you can't describe it as a unique multiple twin. It should be considered as a set of several (3 or 4) reflection twins according secant mirror planes that cut at the same axis.
This model fits some real rutile specimens showing a vvvvv shape, where the rotational model is unsuitable, and many cyclic sixlings that present some overlaps or imperfect joinings at the point where both tails should complete the cycle, and some mixed specimen (cyclic sets containing some vvv twins, see picture).
What about rutile eigthlings? If the angle is 45º, then you can define a valid twinning lattice with a 4-fold axis. But I'm not sure that actual rutile eigthlings have 45º angles...
| Mineral: | Rutile |
| Locality: | | Brazil |  |
|
| Dimensions: | 6 x 6 x 7 cm. |
| Description: |
Brazilian rutile sixling combining many twins with different handedness: look at the striation and follow the lines... The rotational model is unsuitable, but it can be described as a sequence of reflections.
The specimen belongs to Paco from Cantabria (Spain): http://www.foro-minerales.com/forum/viewtopic.php?p=96534#96534 . |
|
| Viewed: |
37362 Time(s) |

|
_________________
Pablo Rodríguez Cantos
Λίθον˛ον απεδοκίμασαν˛οι οικοδομουντες |
|
| Back to top |
|
 |
Pete Richards
Site Admin

Joined: 29 Dec 2008
Posts: 843
Location: Northeast Ohio



|
 Posted: Sep 28, 2015 16:56 Post subject: Re: About cyclic twinning - (5) Posted: Sep 28, 2015 16:56 Post subject: Re: About cyclic twinning - (5) |
|
|
Pablo Cantos has written a very interesting post that provides some useful perspectives on cyclic twins.
The fact that lattices can only have 2, 3, 4, or 6-fold rotational symmetry, when applied to the twin lattice, means that only these exact rotations can define a multiple twin. I have not previously seen the fundamental crystallographic principle of the limits of rotational symmetry applied to the twin lattice, but it is a property of lattices in general so it must apply, to the extent that Friedel's theorem is correct.
It is often convenient to speak of a cyclic twin as having (for example) five-fold symmetry, but this must be understood as an approximation and a convenient way of describing the morphology. As many previous posts have pointed out, such rotational symmetries (including the allowed ones) fail to correctly describe the true crystallographic relationships in specific minerals.
I am hard pressed to think of a twinning situation that I am familiar with where the governing relationship was an n-fold rotation rather than a repeated mirror twinning on some low-index plane such as (110).
I think we idealize and simplify what we see when trying to understand things, and then, armed with an initial conceptual model, tend to seek perfect examples of it - looking for the perfect "hexagonal rutile donut", and considering the rest as imperfect, when they may be screaming that our model is wrong!
Pablo's twin image is a good example - it certainly made some "mistakes" and turned the wrong way, "wasting a lot of good rutile growth before closing out the circle". But all (or nearly all) of those turns presumably conformed to a mirror-twin relationship of twinning on planes of the form {101} (the same thing as {011}).
So in my view, twinning is governed, at least geometrically, by mirror reflections across specific planes. In special circumstances, such twins may approximate, even very closely, rotational symmetries, but the operation of reflection across a lattice plane is what really governs the process.
The question that devils me is: how does this happen in the first place?! Why do we wind up with rutile cycles that approximate a hexagon, or marcasite cycles that approximate a pentagon? What controls when a crystal twins, and how can such controls cause or allow it to twin systematically to close a circle, as opposed to randomly twinning on different faces of the same form, wandering in a random walk across the matrix rather than forming nice closed aggregates? Remembering that twinning usually occurs near the time of crystal nucleation, we may need to think of twinning in all its complexity as a nearly simultaneous process, rather than a sequential one. Do cyclic twins represent self-organization of a sudden nucleation event involving thousands of crystallites at one micro-spot, in which those crystals that are close to a twinning relationship have a growth advantage and engulf the rest? Do linear twinning arrays such as I have seen at Mont Saint-Hilaire represent a titanium-rich solution permeating through a crack in the matrix and suddenly crystallizing, with crystals of one orientation that can form twins having the growth advantage, leading the twinned linear arrays? Frankly, I do not know. But there is apparently a non-randomness in the formation of complex multiple twins, be they cyclic or otherwise, that I understand that I do not understand.
Finally, regarding Pablo's rutile eightlings, I don't know if there is an acceptable "twin lattice" for a four-fold rotational relationship here - unfortunately the software I have will not model such a twin. The relationship still is twinning on {101}, but with perfect oscillation (geometrically) between alternate planes of {101} that creates the zig-zagging necessary to close the octagonal aggregate. I do not know how well repeated twinning on oscillating faces of {101} approximates a perfect octagonal symmetry.
Perhaps someone else can shed some light on this....
_________________
Collecting and studying crystals with interesting habits, twinning, and epitaxy |
|
| Back to top |
|
 |
Pete Richards
Site Admin

Joined: 29 Dec 2008
Posts: 843
Location: Northeast Ohio



|
 Posted: Sep 29, 2015 08:25 Post subject: Re: About cyclic twinning - (5) Posted: Sep 29, 2015 08:25 Post subject: Re: About cyclic twinning - (5) |
|
|
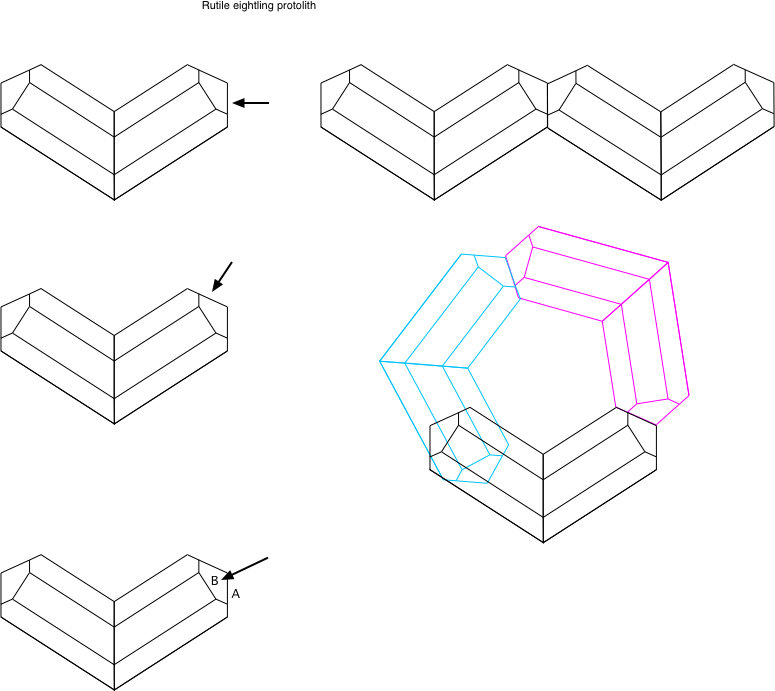
After some head scratching, I think I can comment further on the rutile eightling question. Please realize that this is a geometric exercise, and reflects nothing about the actual growth mechanisms of rutile twins.
Consider a rutile crystal twinned on one plane of {101}, shown in the cartoon as a vertical plane perpendicular to the page - visible as a vertical line. If additional twins are added, the can be added to any of the four faces at the end(s) of the twin. If additional twins are added always on the face that is parallel to the initial twin plane, we get the vvvv twinning pattern that Pablo mentioned.
If additional twins are added always on the face opposite the one that is parallel to the original twin plane, the familiar sixlng is produced. This is shown schematically in the second row.
In order to get an eightling, new twins have to be added in alternating order to a face (call it B) adjacent to the one that is parallel to the original twin plane (call it A), then on A, then B, etc. The sequence ABABABAB produces the eightling.
If this eightling is perfect, the angle between two successive A planes or B planes must be 90°. SHAPE will calculate this angle, even if it can't draw the entire twin. This angle turns out to be 89°54.96'. Very close to 90°, but close does not count in crystallography! So as with the sixling, the eightling fails to have perfect 4-fold rotational symmetry, though the misfit is much smaller.
Again, this is strictly a geometric analysis. It does not purport to say how crystal growth produces a rutile eightling. It also may be the case that in a real eightling the misfit is taken up over more than one twin boundary.
| Description: |
|
| Viewed: |
36809 Time(s) |
|
_________________
Collecting and studying crystals with interesting habits, twinning, and epitaxy |
|
| Back to top |
|
 |
|





