| View previous topic :: View next topic |
| Author |
Message |
Duncan Miller

Joined: 25 Apr 2009
Posts: 138
Location: South Africa



|
 Posted: May 06, 2018 01:11 Post subject: Hematite twins (article in Rocks & Minerals Jan/Feb 2018) Posted: May 06, 2018 01:11 Post subject: Hematite twins (article in Rocks & Minerals Jan/Feb 2018) |
|
|
This is a question for Peter Richards. I have been reading your beautifully illustrated article with Mirjan Žorž (in Rocks & Minerals Jan/Feb 2018) about hematite twins from the Kalahari Manganese Field, and am a bit baffled. The penetration twin on {001} I understand. The contact twin on {001} you rightly say is more readily visualised as twinning on {010}. What I don't understand is its equivalence with twinning on {001}. Please could I ask you to help with some additional explanation.
Edit: Actually I think I have got it now. With reference to the drawing in Figure 3, one half of the crystal is reflected in (001), which is equivalent to a rotation of 180 degrees around [010]. Is that correct?
|
|
| Back to top |
|
 |
Pete Richards
Site Admin

Joined: 29 Dec 2008
Posts: 846
Location: Northeast Ohio



|
 Posted: May 13, 2018 19:28 Post subject: Re: Hematite twins (article in Rocks & Minerals Jan/Feb 2018) Posted: May 13, 2018 19:28 Post subject: Re: Hematite twins (article in Rocks & Minerals Jan/Feb 2018) |
|
|
Hi Duncan,
Sorry to be so slow in answering your question. But my "patience" allowed you to figure it out yourself, for the most part!
The article is probably guilty of not providing enough detail to make this easily understood. I'm glad that someone tried to figure it out.
Step one is to observe that, in terms of the structural relationships among the twins, a twin by reflection on {001} is equivalent to a rotation of one portion through 180° about [001], the c-axis. In the case of these diamond-shaped twins, one half is related by that 180° rotation to the other half, so it is the same twin law.
The overall morphology, however, suggests twinning by reflection across {010}, Here the article is careless, in saying that this is the same thing as twinning on {001}. IT IS NOT!
At the level of overall morphology it is, but in detail it is not. Later in the article it is pointed out that the triangular decorations (manifestations of the three-fold symmetry of the underlying crystal structure) point in opposite directions on each half of the twin. This is consistent with twinning by rotation through 180° about [001], but not with reflection across {010}, under which operation the triangles should point in the same direction on each half.
I hope this resolves your sense of confusion. You were right to be confused!
Thanks for catching this!
_________________
Collecting and studying crystals with interesting habits, twinning, and epitaxy |
|
| Back to top |
|
 |
Duncan Miller

Joined: 25 Apr 2009
Posts: 138
Location: South Africa



|
 Posted: May 14, 2018 04:15 Post subject: Re: Hematite twins (article in Rocks & Minerals Jan/Feb 2018) Posted: May 14, 2018 04:15 Post subject: Re: Hematite twins (article in Rocks & Minerals Jan/Feb 2018) |
|
|
Hello Pete
Thanks for responding and your clarification. The inverted triangles are what got me thinking of rotation about [010] = mirror on {001} (which at first I could not visualise at all), but rotation about [001] as you describe has the same effect. It is clear they are not the result of reflection on {010} or they would point in the same direction.
Now, am I correct in thinking the sides of the diamond-shaped contact twins are crystallographically equivalent to second order prism faces (in order for the composition plane to be (010))?
Duncan
|
|
| Back to top |
|
 |
Pete Richards
Site Admin

Joined: 29 Dec 2008
Posts: 846
Location: Northeast Ohio



|
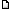 Posted: May 25, 2018 12:24 Post subject: Re: Hematite twins (article in Rocks & Minerals Jan/Feb 2018) Posted: May 25, 2018 12:24 Post subject: Re: Hematite twins (article in Rocks & Minerals Jan/Feb 2018) |
|
|
Hi Duncan,
Your questions have caused me and my co-author to re-examine this kind of twinning, and some of what we stated in the article is incorrect.
In the section where we discuss the diamond-shaped platy twins from Germany and Italy, we stated that they are twins by rotation through 180° about the c-axis [001], with {100} as the composition plane.
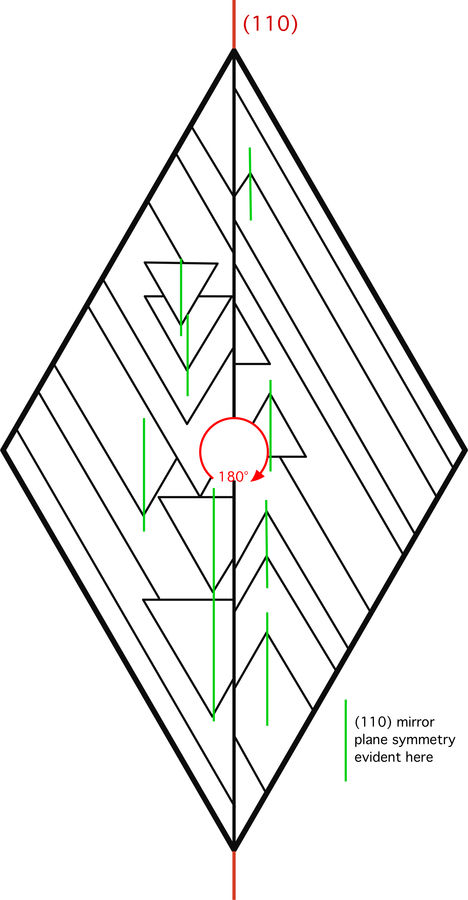
The composition plane of these twins is actually {110}, not {100}. {110} is the plane of mirror symmetry in hematite. The triangular surface patterns in Figure 3 of the article (reproduced with modification below) demonstrate that each individual of the twin has mirror symmetry in the vertical direction as drawn, parallel to the contact surface between the two individuals. The two individuals are not related by this same symmetry relationship, however, because this is not a twin by reflection on {110}. The twin is by rotation about the c-axis, as stated, and {110} only serves as the contact plane.
In fact, reflection across {110} cannot produce a twin in hematite, because {110} is a symmetry element (mirror plane) in the hematite structure itself, and twinning relationships must introduce a new symmetry element, one that is not already present in the untwinned structure.
The attached drawing will hopefully help clarify this.
| Mineral: | Hematite |
| Description: |
| Diagram showing symmetry elements in the diamond-shaped twin. The left half is related to the right half by a 180° rotation, and the two halves are joined along a (110) plane. The edges of the diamond belong to the form {100}. |
|
| Viewed: |
51929 Time(s) |
|
_________________
Collecting and studying crystals with interesting habits, twinning, and epitaxy |
|
| Back to top |
|
 |
Duncan Miller

Joined: 25 Apr 2009
Posts: 138
Location: South Africa



|
 Posted: May 26, 2018 01:35 Post subject: Re: Hematite twins (article in Rocks & Minerals Jan/Feb 2018) Posted: May 26, 2018 01:35 Post subject: Re: Hematite twins (article in Rocks & Minerals Jan/Feb 2018) |
|
|
Hello Pete
Thank you for your clarifiication (and correction), and the new diagram that illustrates the twinning very clearly.
So that others may see where the problem lay, my confusion arose from these sentences in the R & M publication (p 67). "The composition plane of the twin is {010}, which is perpendicular to c{001}. Geometrically, these are perhaps easier to understand as twins on {010}, but crystallographically this is not different from twinning on {001} with a {010} composition surface . . .).
It is tricky for those used to the old (hkil) morphological indexing to visualise the structural indicies, and your labelled diagram is a real help.
Duncan
|
|
| Back to top |
|
 |
|





