| View previous topic :: View next topic |
| Author |
Message |
prcantos
Site Admin
Joined: 17 Apr 2012
Posts: 243
Location: Granada (Spain)



|
 Posted: Jun 08, 2015 17:35 Post subject: Crystallography of Fujian Garnets Posted: Jun 08, 2015 17:35 Post subject: Crystallography of Fujian Garnets |
|
|
Hi. Recently I received this spessartine + feldspar (microcline) + quartz specimen from Fujian (China).
The garnet crystals are really sharp, and the microscope reveals many interesting faces.
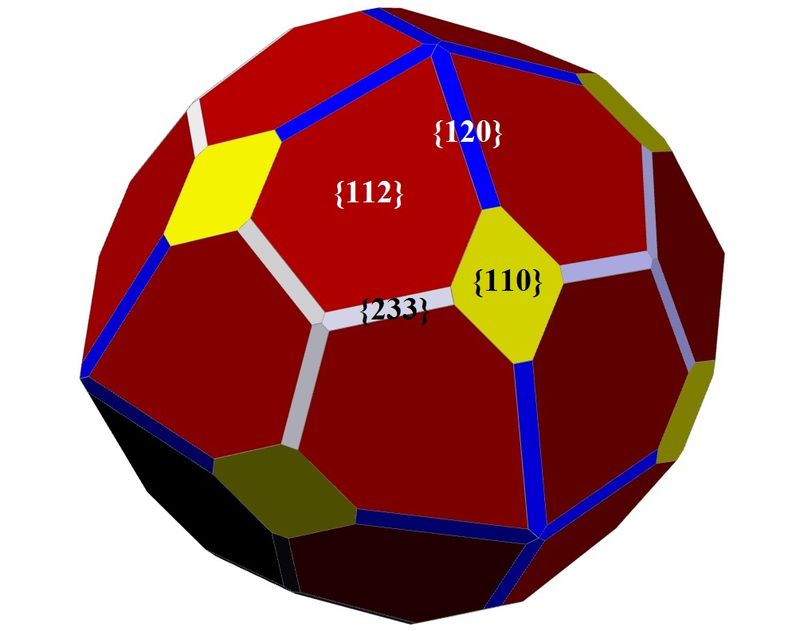
I can recognize the trapezohedron {112}, which is the dominant form, and the rhombdodecahedron {110} (of course I am using minimal Miller indices as I haven't measured the real dihedral angles).
There are apparently other thin faces in the edges of the trapeziums. The thin faces that meet at the 2-fold vertices may be {120} faces (tetrakis-hexahedron), and the ones meeting at the 3-fold vertices might be {233} (triakis-octahedron).
My questions are:
1) Are these thin faces real faces of this crystal, or are they a kind of striation, optical effects, dissolution zones in the crystal...?
2) In case they are true faces, have I identified the forms correctly? I mean: tetrakis-hexahedron faces meeting at the 2-fold vertices and triakis-octahedron faces meeting at the 3-fold vertices.
What do you think? Thank you very much.
| Mineral: | Spessartine, Feldspar (Group), Quartz |
| Locality: | | Wushan Spessartine prospects, Tongbei, Yunxiao, Zhangzhou Prefecture, Fujian Province, China |  |
|
| Dimensions: | 4,5 x 4 cm. |
| Description: |
|
| Viewed: |
20219 Time(s) |

|
| Mineral: | Spessartine |
| Locality: | | Wushan Spessartine prospects, Tongbei, Yunxiao, Zhangzhou Prefecture, Fujian Province, China |  |
|
| Dimensions: | 4 mm. width |
| Description: |
| The main garnet crystal showing many faces. |
|
| Viewed: |
20190 Time(s) |

|
| Mineral: | Spessartine |
| Locality: | | Wushan Spessartine prospects, Tongbei, Yunxiao, Zhangzhou Prefecture, Fujian Province, China |  |
|
| Dimensions: | 60X |
| Description: |
| Micro showing the thin faces in the same garnet. |
|
| Viewed: |
20174 Time(s) |

|
| Mineral: | Spessartine |
| Locality: | | Wushan Spessartine prospects, Tongbei, Yunxiao, Zhangzhou Prefecture, Fujian Province, China |  |
|
| Dimensions: | 60X |
| Description: |
| A darker picture. Thin true? faces at the edges. |
|
| Viewed: |
20198 Time(s) |

|
| Mineral: | Spessartine |
| Locality: | | Wushan Spessartine prospects, Tongbei, Yunxiao, Zhangzhou Prefecture, Fujian Province, China |  |
|
| Dimensions: | 60X |
| Description: |
|
| Viewed: |
20203 Time(s) |

|
| Description: |
| My suggestion for the faces: do you agree? Red = trapezohedron, yellow = rhomdodecahedron, blue = tetrakis-tetrahedron, white = triakis-octahedron. |
|
| Viewed: |
20284 Time(s) |
|
_________________
Pablo Rodríguez Cantos
Λίθον˛ον απεδοκίμασαν˛οι οικοδομουντες |
|
| Back to top |
|
 |
Bob Carnein
Joined: 22 Aug 2013
Posts: 354
Location: Florissant, CO



|
 Posted: Jun 08, 2015 18:19 Post subject: Re: Crystallography of Fujian Garnets Posted: Jun 08, 2015 18:19 Post subject: Re: Crystallography of Fujian Garnets |
|
|
| It looks to me like there are actually 2 faces on each of the"edges" you refer to. If that's the case, then 6 faces meet at the end of each 3-fold axis. Because there are 8 "ends" of 3-fold axes, that would total 48 faces, making the form a hexoctahedron.
|
|
| Back to top |
|
 |
marco campos-venuti

Joined: 09 Apr 2014
Posts: 227
Location: Sevilla



|
 Posted: Jun 09, 2015 02:37 Post subject: Re: Crystallography of Fujian Garnets Posted: Jun 09, 2015 02:37 Post subject: Re: Crystallography of Fujian Garnets |
|
|
The 110 faces look to be responsible for the striation.
| Mineral: | Spessartite Garnet |
| Locality: | | Tongbei, Yunxiao, Zhangzhou Prefecture, Fujian Province, China |  |
|
| Dimensions: | crystal 6 mm |
| Description: |
|
| Viewed: |
20034 Time(s) |

|
| Mineral: | Spessartite Garnet |
| Locality: | | Tongbei, Yunxiao, Zhangzhou Prefecture, Fujian Province, China |  |
|
| Dimensions: | crystal 6 mm |
| Description: |
|
| Viewed: |
20060 Time(s) |

|
|
|
| Back to top |
|
 |
prcantos
Site Admin
Joined: 17 Apr 2012
Posts: 243
Location: Granada (Spain)



|
 Posted: Jun 09, 2015 14:17 Post subject: Re: Crystallography of Fujian Garnets Posted: Jun 09, 2015 14:17 Post subject: Re: Crystallography of Fujian Garnets |
|
|
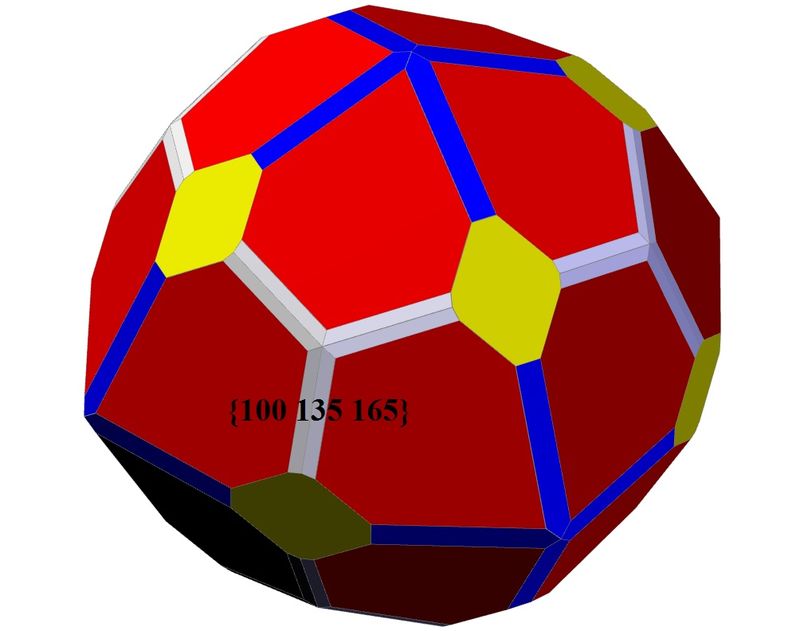
| Bob Carnein wrote: | | It looks to me like there are actually 2 faces on each of the"edges" you refer to. If that's the case, then 6 faces meet at the end of each 3-fold axis. Because there are 8 "ends" of 3-fold axes, that would total 48 faces, making the form a hexoctahedron. |
Thank you, Bob, what a great observation and remark! I have been playing and trying some choices and I have got an approach for the 6-faces vertices: the hexoctahedron {100 135 165} gives almost parallel lines.
Probably there is a different hexoctahedron appearing at the 8-faces vertices, but I haven't estimated it.
Marco, these are really outstanding garnets!!
| Description: |
| A better approach using the hexoctahedron. |
|
| Viewed: |
19985 Time(s) |
|
_________________
Pablo Rodríguez Cantos
Λίθον˛ον απεδοκίμασαν˛οι οικοδομουντες |
|
| Back to top |
|
 |
Pete Richards
Site Admin

Joined: 29 Dec 2008
Posts: 843
Location: Northeast Ohio



|
 Posted: Jun 09, 2015 19:49 Post subject: Re: Crystallography of Fujian Garnets Posted: Jun 09, 2015 19:49 Post subject: Re: Crystallography of Fujian Garnets |
|
|
Let me interject a bit of Miller index algebra into this discussion. This can be documented by reference to many standard texts, and it makes solving such problems much easier!
Rule 1: If you want to find the face that bevels two other faces (i.e. forms a single face that has parallel edges in intersection with them), add the Miller indices, index by index. So for the faces (211) and (21-1), the beveling face is (420)=(210), and this is true for every such edge on the specimen, so the beveling form is {210}. For the faces (211) and (121) - Pablos's second case, the beveling face is (332) as he inferred, and the general form for that bevel is {332}.
Rule 2: Now, if we want not one face modifying an edge but two parallel faces, we can use a more general relationship, that n(hkl1)+m(hkl2) is a form that works for any value of n and m. For example, this could be 3*(211)+2*(121)=6 3 3 + 2 4 2= 8 7 5 = (875). Or one could add one face to the bevel: (211)+(210) = (421) - with any weighting between them via n and m values. Any faces so generated will satisfy the criterion that they are two-fold around the edge in question, and are strictly parallel to this edge. (I should be careful and state that the two-fold statement only applies in certain higher symmetry classes such as garnet, but the strict parallelism applies in all cases).
The question of which form is the right choice then becomes one of what the angles are between the main faces and the beveling faces. Without measurements, this question cannot be answered unambiguously. However, one of the empirical laws of crystallography is that Miller indices of crystal faces tend to be small integers, so Pablo' 100 135 165 is approximately 1.0 1.33 1.67 or (345) when cleared of fractions. (345) is equal to 2*(211)+(121)=4 2 2 + 1 2 1=5 4 3 =(by symmetry) (345), or the form {345}.
It is also interesting to note that no single hexoctahedron can provide double bevels both to the edges that lead to the cube axes and to those that lead to the three-fold axes, coded blue and white in Pablo' first drawing respectively. I cannot prove this algebraically, but geometrically it appears to be quite evident: If you stick in a form that will bevel one of the edges leading to the three-fold axis, it will not bevel the very differently oriented edge leading to the four-fold axis, and vise versa.
If (as I cannot tell) all of these edges have double bevels of roughly equal size and angle, this strongly suggests that these modifying faces are due to dissolution rather than crystal growth, in which case they are not true crystal faces. The irregularity shown in some images tends to reinforce this suggestion.
I think Marco's images show true growth faces with alternation between dodecahedron and trapezohedron, but they are a different issue from Pablo' crystals.
Whew! I almost blew this response away after a half hour of working on it!! Now, fifteen minutes later, I hope you can get some good stuff from it! Meanwhile, for those who are tuned into American basketball, I'm about to go and hope that the Cleveland Cavaliers can win again!
_________________
Collecting and studying crystals with interesting habits, twinning, and epitaxy |
|
| Back to top |
|
 |
marco campos-venuti

Joined: 09 Apr 2014
Posts: 227
Location: Sevilla



|
 Posted: Jun 10, 2015 02:56 Post subject: Re: Crystallography of Fujian Garnets Posted: Jun 10, 2015 02:56 Post subject: Re: Crystallography of Fujian Garnets |
|
|
Your Cleveland Cavaliers won Pete, so probably you are now busy drinking beer and honking your horn in the streets!
When you'll be back I just have a question for you: the faces due to dissolution are not true crystal faces, but they are true crystal lattice faces. So what is the difference? They also have indexes. Or not?
|
|
| Back to top |
|
 |
prcantos
Site Admin
Joined: 17 Apr 2012
Posts: 243
Location: Granada (Spain)



|
 Posted: Jun 10, 2015 08:45 Post subject: Re: Crystallography of Fujian Garnets Posted: Jun 10, 2015 08:45 Post subject: Re: Crystallography of Fujian Garnets |
|
|
| Pete Richards wrote: | | ...The question of which form is the right choice then becomes one of what the angles are between the main faces and the beveling faces. Without measurements, this question cannot be answered unambiguously. However, one of the empirical laws of crystallography is that Miller indices of crystal faces tend to be small integers, so Pablo' 100 135 165 is approximately 1.0 1.33 1.67 or (345) when cleared of fractions. (345) is equal to 2*(211)+(121)=4 2 2 + 1 2 1=5 4 3 =(by symmetry) (345), or the form {345}... |
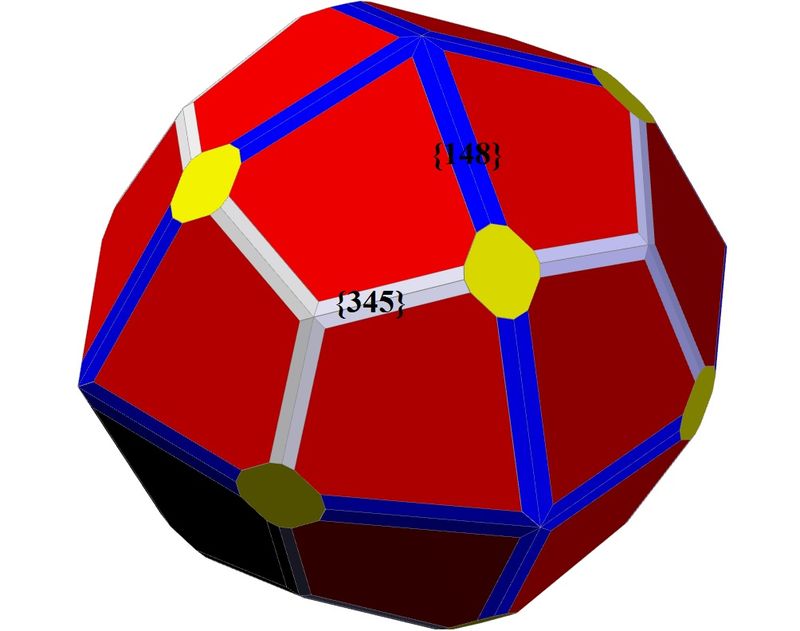
Thank you, Peter, for this answer. Really I needn't know the exact indices, determine the form is good enough for me. I have drawn another diagram using your approximation {345} and a new hexoctahedron {148} that fits what we can see in the crystal.
| Pete Richards wrote: | | ...It is also interesting to note that no single hexoctahedron can provide double bevels both to the edges that lead to the cube axes and to those that lead to the three-fold axes, coded blue and white in Pablo' first drawing respectively. I cannot prove this algebraically, but geometrically it appears to be quite evident: If you stick in a form that will bevel one of the edges leading to the three-fold axis, it will not bevel the very differently oriented edge leading to the four-fold axis, and vise versa. |
This is a very interesting problem. I would like to think about it more carefully...
| Pete Richards wrote: | | ... If (as I cannot tell) all of these edges have double bevels of roughly equal size and angle, this strongly suggests that these modifying faces are due to dissolution rather than crystal growth, in which case they are not true crystal faces. The irregularity shown in some images tends to reinforce this suggestion... |
I usually think that crystals have some planes where "everything happens": cleavage, twinning, crystal faces, dissolution processes... Maybe they are "weakness planes" according to molecular structure, and of course they have low or simple Miller indices. Anyway this is only a feeling, I haven't studied it.
| Description: |
| The third estimation using two different hexoctahedra: {345} and {148}. |
|
| Viewed: |
19802 Time(s) |
|
_________________
Pablo Rodríguez Cantos
Λίθον˛ον απεδοκίμασαν˛οι οικοδομουντες |
|
| Back to top |
|
 |
Pete Richards
Site Admin

Joined: 29 Dec 2008
Posts: 843
Location: Northeast Ohio



|
 Posted: Jun 10, 2015 12:21 Post subject: Re: Crystallography of Fujian Garnets Posted: Jun 10, 2015 12:21 Post subject: Re: Crystallography of Fujian Garnets |
|
|
| marco campos-venuti wrote: | Your Cleveland Cavaliers won Pete, so probably you are now busy drinking beer and honking your horn in the streets!
When you'll be back I just have a question for you: the faces due to dissolution are not true crystal faces, but they are true crystal lattice faces. So what is the difference? They also have indexes. Or not? |
Actually, Marco, the basketball finals are a best-of-seven (or first team with four wins) format, so, sure, I had a beer, but will save the horn for later.
Your question about dissolution faces is a good one. My perspective is that dissolution forms are usually not really flat, but are curved, pitted, etc. Since Miller indices describe the orientation of a PLANE, these forms do not have unique indices. Now one can argue that many growth faces are not strictly planar either, and I know of examples where such growth faces deviate from being planar quite drastically. One can only then talk about Miller indices that describe the approximate or "average" orientation of the face. Such non-planar growth faces at least tend to be smooth at a fine scale (smoothly curved), while this is often not the case with dissolution forms. There are certainly occasions where it is difficult to decide whether a particular face is due to growth or to dissolution.
The other thing to consider, and this responds to Pablo's last post as well, is that generally growth and dissolution can be considered inverse processes. Dissolving is "un-growing". Faces that grow rapidly tend to grow themselves out of existence; these tend to be faces with large Miller indices. However, those same orientations are directions also of rapid dissolution. For that reason dissolution facets tend to occur along edges and at corners of crystals, and may have high indices, if one can even assign approximate indices to them.
_________________
Collecting and studying crystals with interesting habits, twinning, and epitaxy |
|
| Back to top |
|
 |
prcantos
Site Admin
Joined: 17 Apr 2012
Posts: 243
Location: Granada (Spain)



|
 Posted: Jun 11, 2015 04:50 Post subject: Re: Crystallography of Fujian Garnets Posted: Jun 11, 2015 04:50 Post subject: Re: Crystallography of Fujian Garnets |
|
|
| prcantos wrote: | | 1) Are these thin faces real faces of this crystal, or are they a kind of striation, optical effects, dissolution zones in the crystal...? |
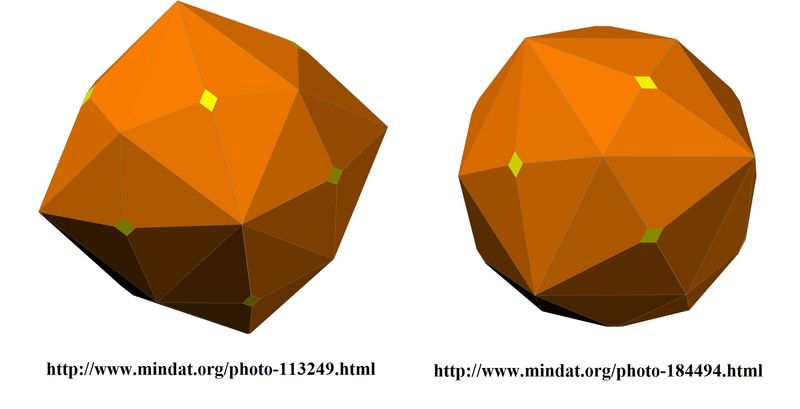
Though we can't say if these presumed faces are in fact true faces, I have found some pictures in Mindat that show that this locality produces garnets with evident hexoctahedral faces or even complete hexoctahedra!
https://www.mindat.org/photo-113249.html
https://www.mindat.org/photo-184494.html
These specimens show a dominant hexoctahedron with some vertices truncated by the dodecahedron. Compare the pictures in Mindat to the drawings below.
So I can be inclined to think that the crystals we have studying here could have true hexoctahedral faces.
| Description: |
Diagrams for some hexoctahedral garnets from Fujian in Mindat.
Left: http://www.mindat.org/photo-113249.html
Right: http://www.mindat.org/photo-184494.html |
|
| Viewed: |
19693 Time(s) |
|
_________________
Pablo Rodríguez Cantos
Λίθον˛ον απεδοκίμασαν˛οι οικοδομουντες |
|
| Back to top |
|
 |
|




