prcantos
Site Admin
Joined: 17 Apr 2012
Posts: 243
Location: Granada (Spain)



|
 Posted: Aug 26, 2013 11:31 Post subject: Real examples for 'glide reflection' twins? Posted: Aug 26, 2013 11:31 Post subject: Real examples for 'glide reflection' twins? |
|
|
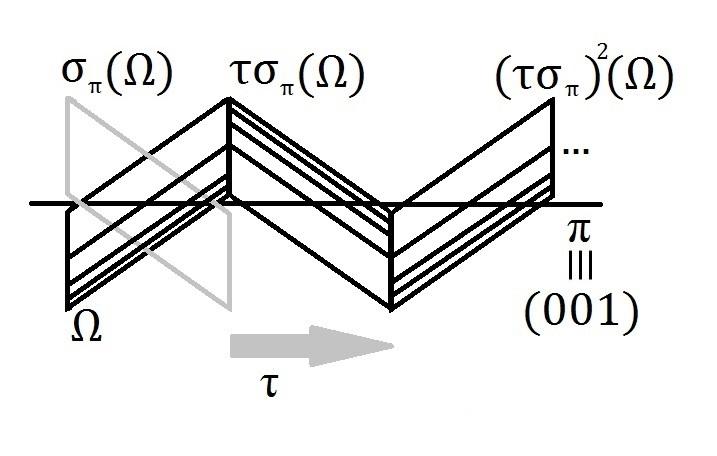
Hi. Recently I have been studying twinning using an algebraic approach in the Spanish-side FMF. I have used the mathematical classification of rigid motions in affine space to propose a tipology for twinning, but I have realized there is one of the seven types in the classification which doesn't fit any real example, as far as I can know.
This rigid motion is called 'glide reflection'. It consists of a plane symmetry followed by a translation, so that the translation vector is parallel to the symmetry plane.
As a failed example, I give you an scheme of the geniculated twin of rutile to show how this glide reflection works. I thought this twin is generated by the symmetry σ_π followed by the translation τ (an alternative description to sucessive rotations), but later I realized that such a description is invalid: look at the striae-lines!
Thus I have no example at all for this rigid motion. Do you know a real twin in a mineral species than can be described this way? Or could you imagine some possibilities at least? Really thanks to you!
| Description: |
| A wrong description of geniculated rutile twin using glide reflection |
|
| Viewed: |
7147 Time(s) |
|
_________________
Pablo Rodríguez Cantos
Λίθον˛ον απεδοκίμασαν˛οι οικοδομουντες |
|
Pete Richards
Site Admin

Joined: 29 Dec 2008
Posts: 846
Location: Northeast Ohio



|
 Posted: Sep 05, 2013 13:08 Post subject: Re: Real examples for 'glide reflection' twins? Posted: Sep 05, 2013 13:08 Post subject: Re: Real examples for 'glide reflection' twins? |
|
|
It seems to me that the rutile example you provided is actually a correct example. I do not see why you have extra faces on one side of the generating prism; they are not consistent with rutile symmetry. I see that you mean them to be striations, but since striations are just growth features, they do not need to conform to symmetry operation, whether of the crystal itself or of a twinning operator.
However, this morphology (without the extra faces or striations) could also result from simple reflection about the vertical plane. I suppose this just shows that more than one operator can produce the same results, especially when the object itself has symmetry properties as well.
Thus, for example, a spinel-twinned octahedron of spinel is identical whether the operator is reflection across the 111 plane or rotation about an axis perpendicular to it. However, in sphalerite, the "octahedron" is composed of two tetrahedra, one positive and one negative, with different surface chemistry and often different luster. Reflection causes faces of the same type to be opposite each other across the twin plane, while rotation causes faces of opposite types to be opposite each other - these two twin operators produce different results because of sphalerite's lower symmetry.
I don't understand the notation 001. The plane in question for rutile would be 101, and 001 would be perpendicular to the prism's long direction.
I hasten to add that, while this is an interesting exercise in describing the overall morphology of twins, twinning really occurs at the atomic level, and this description is inconsistent with the way twinned crystals grow.
This is consistent with some of the old ideas about twinning (e.g. the metagenetic twin of Dana's Textbook, article 245), in which a crystal grows for awhile, then suddenly twins and grows some more, and perhaps does so many times. Such twinning, I have argued, is rare to non-existent in actual twinned crystals.
_________________
Collecting and studying crystals with interesting habits, twinning, and epitaxy |
|




