| View previous topic :: View next topic |
| Author |
Message |
prcantos
Site Admin
Joined: 17 Apr 2012
Posts: 243
Location: Granada (Spain)
|
 Posted: Feb 26, 2015 16:35 Post subject: Re: Classification of crystallographic forms - using matrices |
|
|
| prcantos wrote: | | ...I will show you some examples of this algebraic approach and explain some troubles I find. |
Now I am going to show my attempt to classify the forms using matrices. The method consists of two stages:
Stage A) You have to construct a matrix which resumes the symmetry of the point group in certain sense. This is the inventive part.
Stage B) You have to study that matrix using an accurate matricial method. This is the technical part.
Here you have a very easy example involving a low-symmetry group G=4 (tetragonal-pyramidal class).
G=4 is a cyclic group generated by the 4-fold rotation around [001] axis. Let ρ be that symmetry operation. Thus G={1,ρ,ρ^2,ρ^3}, where 1 is the identity operation. If B_0 is the usual orthonormal basis of R^3, the matrix for ρ is the matrix M in the first picture.
Stage A) Let us construct a 3x3 squared matrix A that resumes the symmetry of G. Let (h,k,l) be an arbitrary vector in R^3 (you can pick it on the unit sphere as well). Using M we calculate ρ(h,k,l) and ρ^2(h,k,l). These resultant vectors will be the second and the third column of A. The first column will be 1(h,k,l)=(h,k,l). The columns of the matrix A contain the essential information of the action of G applied to the arbitrary vector (h,k,l).
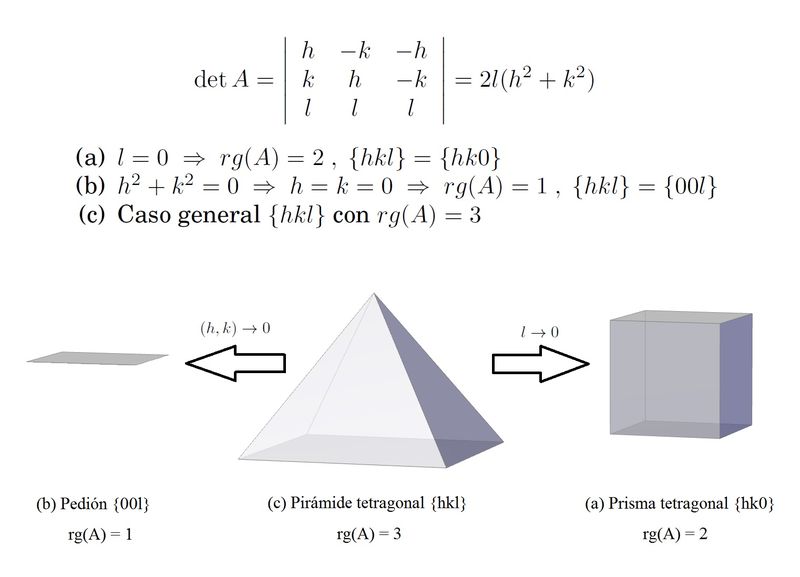
Stage B) This matrix is supposed to be useful to classify the forms for G. In this simple case we can discuss the rank of A (2nd picture) solving the equation det A = 0. We obtain the three possible forms matched to the three possible values for the rank. The general form is the tetragonal pyramid (rank 3), and two special forms: the tetragonal prism (rank 2) and the pedion (rank 1).
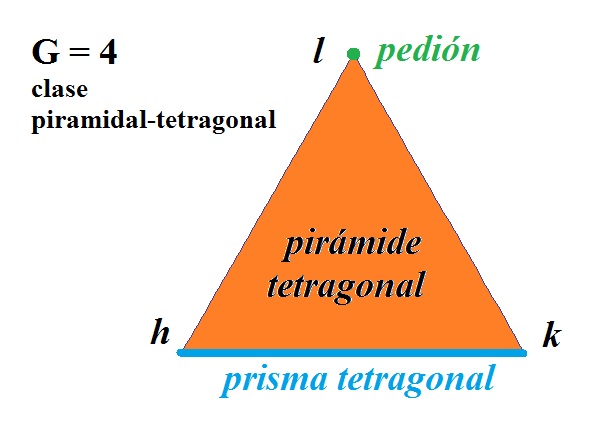
Finally we can represent this result in the {hkl}-diagram (3rd picture).
| Description: |
| Preparing the matrix A... |
|
| Viewed: |
47743 Time(s) |
|
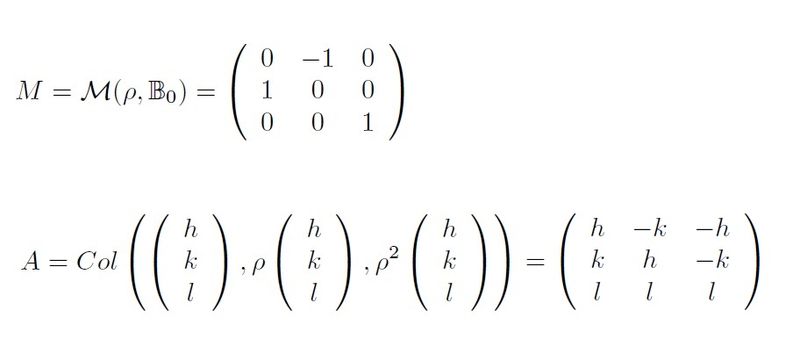
| Description: |
| Discussing the ranks and identifying the resultant forms... |
|
| Viewed: |
47781 Time(s) |
|
| Description: |
| Showing the results in the {hkl}-triangle... |
|
| Viewed: |
47866 Time(s) |
|
_________________
Pablo Rodríguez Cantos
Λίθον˛ον απεδοκίμασαν˛οι οικοδομουντες |
|
| Back to top |
|
 |
Roger Warin
Joined: 23 Jan 2013
Posts: 1233
|
| Posted: Feb 26, 2015 17:13 Post subject: Re: Classification of crystallographic forms - any references? |
|
|
Hi Pete
Thank you for sharing this concept. I had not thought to consider in this respect the distribution of all forms of calcite. I am even surprised with the results.
I think this projection deserves a new topic with comments about this new milky way. Many thanks.
Roger.
|
|
| Back to top |
|
|
Pete Richards
Site Admin
Joined: 29 Dec 2008
Posts: 845
Location: Northeast Ohio
|
| Posted: Feb 26, 2015 17:23 Post subject: Re: Classification of crystallographic forms - any references? |
|
|
Thanks Roger,
I agree this could be a whole new direction in these discussions, and I could add more. I do not know how to branch a thread - perhaps our chief guru Jordi can do this. I'll be glad to participate!
_________________
Collecting and studying crystals with interesting habits, twinning, and epitaxy |
|
| Back to top |
|
|
prcantos
Site Admin
Joined: 17 Apr 2012
Posts: 243
Location: Granada (Spain)
|
| Posted: Feb 27, 2015 05:07 Post subject: Re: Classification of crystallographic forms - any references? |
|
|
Peter, perhaps you could start a new thread for the calcite forms topic. Or maybe you prefer to write a 'theoretic approach' in this outstanding thread containing many pictures:
Calcite Forms - (4).
Both would be a really interesting topic!
Please let me make just some remark or question about calcite 'forms'. The word 'form' in Crystallography means 'a set of equivalent faces' according to symmetry relations. Thus calcite can only show these 6 forms, the only possible for G=-32/m (Hexagonal Scalenohedral class): pinacoid, hexagonal prism, rhombohedron, hexagonal dypiramid, hexagonal scalenohedron and dihexagonal prism (cf. 'Dana' op. cit. p 91, table after Buerger op. cit.).
The rest of 'global configurations' of faces in crystals should be called with a different term I think, but not 'form'. Do you think so?
_________________
Pablo Rodríguez Cantos
Λίθον˛ον απεδοκίμασαν˛οι οικοδομουντες |
|
| Back to top |
|
|
Pete Richards
Site Admin
Joined: 29 Dec 2008
Posts: 845
Location: Northeast Ohio
|
| Posted: Feb 27, 2015 10:13 Post subject: Re: Classification of crystallographic forms - any references? |
|
|
| prcantos wrote: |
Please let me make just some remark or question about calcite 'forms'. The word 'form' in Crystallography means 'a set of equivalent faces' according to symmetry relations. Thus calcite can only show these 6 forms, the only possible for G=-32/m (Hexagonal Scalenohedral class): pinacoid, hexagonal prism, rhombohedron, hexagonal dypiramid, hexagonal scalenohedron and dihexagonal prism (cf. 'Dana' op. cit. p 91, table after Buerger op. cit.).
The rest of 'global configurations' of faces in crystals should be called with a different term I think, but not 'form'. Do you think so? |
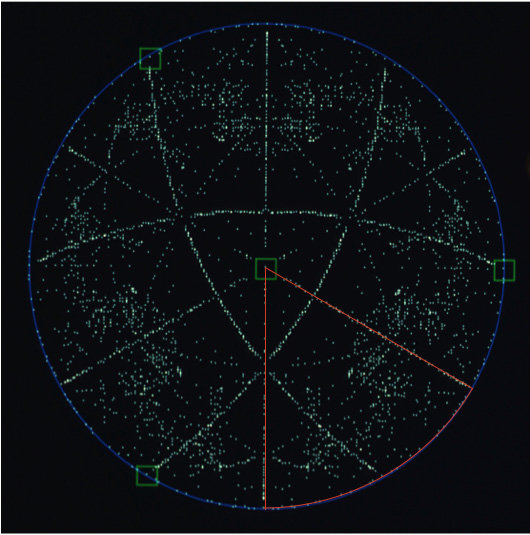
Pablo, you are right. What my stereographic projection really shows is the the poles in the upper hemisphere of the faces of all known forms of calcite. So dihexagonal prisms are represented by 12 dots (all along the bounding circle), scalenohedra, prisms, and hexagonal dipyramids are represented by 6 dots, rhombohedra by 3, and the pinacoid by 1.
The region representing the forms, if it is assumed that the forms have their usual indices (e.g. (21-31) and not the equivalent (-3211), is the region bordered by red in this modified diagram.
I think showing the whole hemisphere is more interesting and more pleasing, because it really depicts the symmetry as it acts to replicate faces.
| Description: |
|
| Viewed: |
47741 Time(s) |
|
_________________
Collecting and studying crystals with interesting habits, twinning, and epitaxy |
|
| Back to top |
|
|
prcantos
Site Admin
Joined: 17 Apr 2012
Posts: 243
Location: Granada (Spain)
|
| Posted: Mar 05, 2015 06:06 Post subject: Re: Classification of crystallographic forms - any references? |
|
|
Maybe I have found an answer to one of my previous questions: why are we using some dashed-lines matching symmetry elements which don't belong to the consider symmetry group? If they don't belong to the group they wouldn't be used to classify the forms.
The answer is related to 'Wyckoff positions' and 'crystallographic orbits'. These are concepts that appear in the study of space groups and can be transferred to point groups.
I haven't studied space groups before, but I am doing it now. I will tell you what I learn.
_________________
Pablo Rodríguez Cantos
Λίθον˛ον απεδοκίμασαν˛οι οικοδομουντες |
|
| Back to top |
|
|
prcantos
Site Admin
Joined: 17 Apr 2012
Posts: 243
Location: Granada (Spain)
|
| Posted: Mar 06, 2015 11:11 Post subject: Re: Classification of crystallographic forms - any references? |
|
|
Meanwhile I add a new example of the matricial calculations of the forms for the group G=4/m, with the same notation and procedures. The columns in the matrix A are the images of (h,k,l) by identity, the 4-fold Z-axis rotation ρ and the XY-mirror symmetry σ.
| Description: |
| The matrix A resumes the symmetry of the group G=4/m. |
|
| Viewed: |
8853 Time(s) |
|
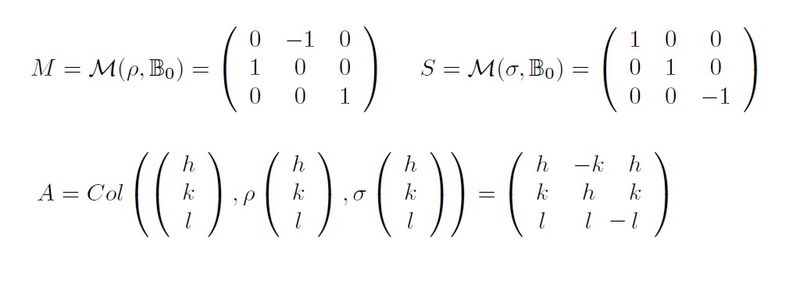
| Description: |
| Discussion and resultant forms. Obviously the prism is an open form (without bases). |
|
| Viewed: |
8815 Time(s) |
|
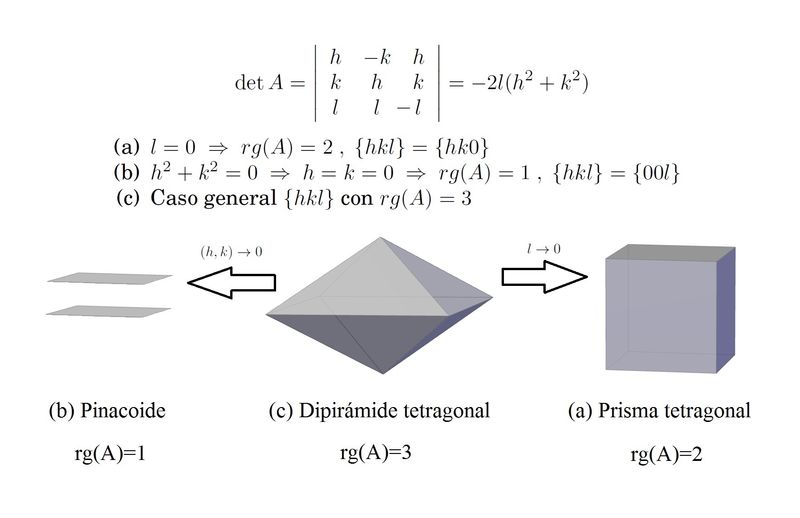
| Description: |
| Representation of the forms in the (h,k,l)-triangle. |
|
| Viewed: |
8800 Time(s) |
|
_________________
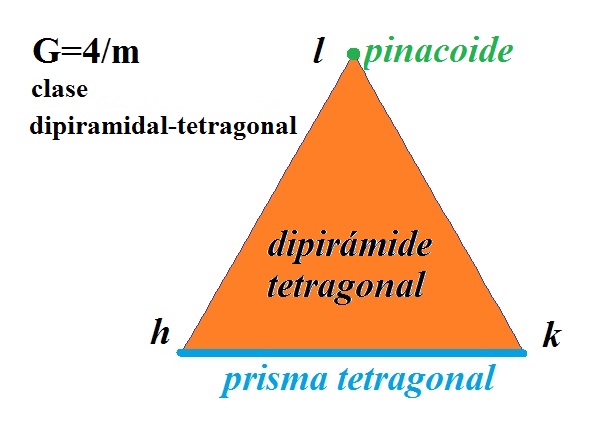
Pablo Rodríguez Cantos
Λίθον˛ον απεδοκίμασαν˛οι οικοδομουντες |
|
| Back to top |
|
|
|
FAQ 
Register
Log in
Forgotten your password?
