| View previous topic :: View next topic |
| Author |
Message |
Tracy

Joined: 15 Sep 2006
Posts: 551
Location: Toronto



|
 Posted: Aug 18, 2012 08:39 Post subject: About cyclic twinning - (5) Posted: Aug 18, 2012 08:39 Post subject: About cyclic twinning - (5) |
|
|
I recently saw an image of a rutile specimen described as a cyclic twin, however the specimen wasn't round - rather, it looked like a series of steps or a "w" with a few extra bends (vvv-like). Was this an accurate description? I would expect a cyclic twin to be cyclic (= ring-shaped), but was wondering what are the criteria?
- Tracy
_________________
"Wisdom begins in wonder" - Socrates |
|
| Back to top |
|
 |
gemlover

Joined: 31 Dec 2008
Posts: 211
Location: Easley, SC



|
 Posted: Aug 18, 2012 13:54 Post subject: Re: About cyclic twinning - (5) Posted: Aug 18, 2012 13:54 Post subject: Re: About cyclic twinning - (5) |
|
|
To me cyclic would be a repeating pattern in a form of circular crystal axis, not necessarily round, if hexagons are cyclic then they would have flat sides around the outside of the sample. I'm not sure if the is understandable, but think of a benzene ring, it has "flat" sides, and organic molecules that are "cyclic" have a repeating pattern around an axis.
john
_________________
John
John Atwell Rasmussen, Ph.D.. AJP
Geologist and Gemologist |
|
| Back to top |
|
 |
Tracy

Joined: 15 Sep 2006
Posts: 551
Location: Toronto



|
 Posted: Aug 18, 2012 18:22 Post subject: Re: About cyclic twinning - (5) Posted: Aug 18, 2012 18:22 Post subject: Re: About cyclic twinning - (5) |
|
|
I think of the term "cyclic" as in chemistry too, which is why I was wondering. There definitely was some twinning happening (though I can't confirm that it was continuous) but not all in the same direction....in chem-speak, like an aliphatic chain. Of course, I couldn't say for certain that the twinning was all of the same crystal.
- Tracy
_________________
"Wisdom begins in wonder" - Socrates |
|
| Back to top |
|
 |
Pete Richards
Site Admin

Joined: 29 Dec 2008
Posts: 846
Location: Northeast Ohio



|
 Posted: Aug 18, 2012 18:34 Post subject: Re: About cyclic twinning - (5) Posted: Aug 18, 2012 18:34 Post subject: Re: About cyclic twinning - (5) |
|
|
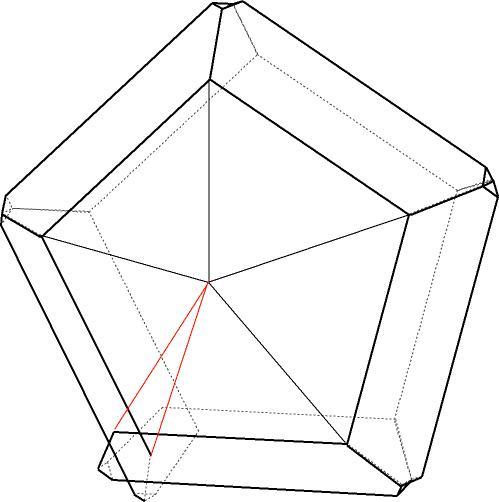
A cyclic twin is one in which the repeated application of the twin law leads to the formation of a closed loop. Rutile can do this in two ways. In one case you get a "hexagonal bagel" composed of six individuals. In the other case you get an "octagonal waffle" composed of eight individuals zig-zagging back and forth, as referenced in the initial posting.
Cyclic twinning can also occur in many other minerals: aragonite famously, but also marcasite and many others. In the case of marcasite, the twin aggregate has five individuals twinned on {101} (relative to a unit cell with a:b:c=.8194:1:.6245) laid out like a pentagon. However, when the cycle completes, the "last" join is not perfect, but the two joining individuals overlap each other.
A tricky thing about cyclic twinning is that it does not occur cyclically. That is to say, one crystal does not form, then twin off another, which then twins off another, until the cycle is complete. Rather, cyclic twins almost certainly develop simultaneously by self-organization of a poly-crystalline nucleus early in crystal growh. The polycrystalline mass eliminates many individuals and the remaining ones are in twinned orientation, or nearly so. This is my own opinion; I'm not sure I've ever seen it in the literature.
In the sequential ("cyclic") twinning model, for example, with rutile each twinning step has four possible directions to go. Only one of them at each twinning step will lead to a complete cyclic twin; the rest lead to chaotic kinked "worms". This suggests that only one in 4^5 = 1024 rutile crystals that contain six twinned individuals will complete the cycle in a "one at a time" twinning model, and only one in 4^7 = 16,384 eightlings will form the zig-zag cycle. On top of that, sixlings are the cyclic twins found exclusively in some localities, while eightlings are found in other localities without the "more probable" sixlings. Maybe we just ignore all the rest and look very carefully for these exceptions, or maybe there's an organizing principle that makes them much more likely to occur.
An additional possible orienting principle is epitactic overgrowth on another mineral. For example, rutile growing epitactically on and parallel to the edges of a hematite crystal would form a sixling. One would have to envision a separate relationship of this sort for each mineral, however.
The formation of cyclic twins is, I think, poorly understood, and a fascinating area for more research. There may, however, be good papers in languages other than English that I am not aware of. I would welcome citations of useful papers, regardless the language!
| Description: |
| Hypothetical cyclic twin of marcasite. The red lines indicate the overlap that would occur if all the misfit in the cycle were accommodated in this one juncture. |
|
| Viewed: |
74855 Time(s) |
|
_________________
Collecting and studying crystals with interesting habits, twinning, and epitaxy |
|
| Back to top |
|
 |
Pete Richards
Site Admin

Joined: 29 Dec 2008
Posts: 846
Location: Northeast Ohio



|
 Posted: Aug 18, 2012 18:50 Post subject: Re: About cyclic twinning - (5) Posted: Aug 18, 2012 18:50 Post subject: Re: About cyclic twinning - (5) |
|
|
I think comparisons to things like benzene rings are quite misleading. I'm not an organic chemist, but please remember that crystals consist of a basic structure which is repeated in three dimensions "into infinity". The basic structure may contain linked building blocks like silicate tetrahedra, but until the structure itself gets replicated through space it is not a crystal. A benzene ring is a single entity. To become a crystal, it must be somehow stacked in three dimensions, with something to hold it together. This may happen in certain (very cold) environments, but it is not the way we typically think of organic chemicals.
In twinned crystals, the basic extended structure is related from one piece of the twin to another (usually) across a plane (called the twin plane) which separates an individual with its structure in one orientation from another individual with another orientation. The twin plane is not a symmetry element of the basic structure (otherwise it would not change the structure's orientation) but typically has an orientation that brings the two individuals together in an energetically favorable orientation.
Penetration twins are a matter for another day....
_________________
Collecting and studying crystals with interesting habits, twinning, and epitaxy |
|
| Back to top |
|
 |
John S. White
Site Admin

Joined: 04 Sep 2006
Posts: 1298
Location: Stewartstown, Pennsylvania, USA



|
 Posted: Aug 19, 2012 06:02 Post subject: Re: About cyclic twinning - (5) Posted: Aug 19, 2012 06:02 Post subject: Re: About cyclic twinning - (5) |
|
|
I was hoping that Pete Richards would enter this discussion and I am pleased to see that he has done so. I tend to agree with him but as far as I know he can find very little support for his definition in the literature. In fact, the only reference I can find in my library is Sinkankas' Mineralogy, in which John has written "Cyclic twins develop when crystals twin on several sides at once, curving around to form disk-like or doughnut-shaped groups or groups of even greater complexity." However, in his illustrations he labels the familiar pseudo-hexagonal aragonite twins as penetration twins, not cyclic twins. This seems to me to be inconsistent and confuses the issue.
_________________
John S. White
aka Rondinaire |
|
| Back to top |
|
 |
John S. White
Site Admin

Joined: 04 Sep 2006
Posts: 1298
Location: Stewartstown, Pennsylvania, USA



|
 Posted: Aug 19, 2012 06:14 Post subject: Re: About cyclic twinning - (5) Posted: Aug 19, 2012 06:14 Post subject: Re: About cyclic twinning - (5) |
|
|
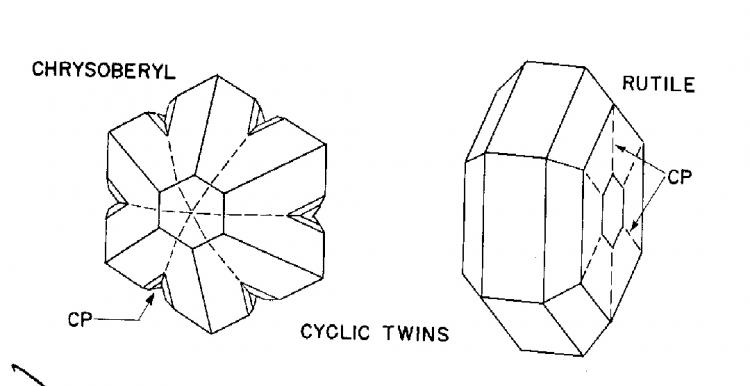
Some lillustrations from John Sinkankas' book Mineralogy
| Description: |
|
| Viewed: |
74739 Time(s) |
|
_________________
John S. White
aka Rondinaire |
|
| Back to top |
|
 |
Tracy

Joined: 15 Sep 2006
Posts: 551
Location: Toronto



|
 Posted: Aug 19, 2012 07:32 Post subject: Re: About cyclic twinning - (5) Posted: Aug 19, 2012 07:32 Post subject: Re: About cyclic twinning - (5) |
|
|
Thanks Pete for the explanation. It sounds to me as though the defining characteristic of a cyclic twin is loop closure, versus the kinked worm. The specimen I saw has six distinct faces, appears to be planar or nearly so, and originates from Diamantina. Does this information help determine whether or not it is a cyclic twin?
...with apologies for the chem-speak, but imagining a bonded carbon atom in 3D it is easy to visualize the 4 branches to which I think you are referring.
- Tracy
_________________
"Wisdom begins in wonder" - Socrates |
|
| Back to top |
|
 |
simonoff
Joined: 16 Feb 2009
Posts: 161


|
 Posted: Aug 19, 2012 15:13 Post subject: Re: About cyclic twinning - (5) Posted: Aug 19, 2012 15:13 Post subject: Re: About cyclic twinning - (5) |
|
|
Kind of funny Tracy you seem to be describing a piece that I just recently posted on a photo sharing site, instagram. I am trying to share minerals and the little knowledge I have with that audience. On august 18 I posted several cyclic twins from the Smithsonian.
Bob
|
|
| Back to top |
|
 |
Dean Allum

Joined: 27 Jan 2010
Posts: 17
Location: Colorado


|
 Posted: Aug 20, 2012 13:09 Post subject: Re: About cyclic twinning - (5) Posted: Aug 20, 2012 13:09 Post subject: Re: About cyclic twinning - (5) |
|
|
Pete,
Your competing poly-crystals theory for cyclic twinning is elegant!
Wouldn't there be some remaining evidence of the nucleation site at the central vertex which you could view with a TEM of the thin section?
-Dean Allum
|
|
| Back to top |
|
 |
Pete Richards
Site Admin

Joined: 29 Dec 2008
Posts: 846
Location: Northeast Ohio



|
 Posted: Aug 20, 2012 13:27 Post subject: Re: About cyclic twinning - (5) Posted: Aug 20, 2012 13:27 Post subject: Re: About cyclic twinning - (5) |
|
|
1) John White raises an interesting issue that I had not thought of – cyclic twins as penetration twins rather than contact twins. In the cyclic twinning model I presented earlier, one crystal gives rise to another crystal by twinning, and this one gives rise to yet another by the same twin law, and so forth until the cycle reaches a closed form. I alluded earlier to the conceptual problem when this process leads to an overlap (or a gap) at the end of the cycle, and as well to the discordance between this model and our understanding of how crystals typically grow.
(The normal thinking about twinning is that it occurs at the very beginning of crystal growth. To the extent that this is true, cyclic twins arise all at once at crystal nucleation, whether by the “self-organizing” approach I mentioned earlier or by the nucleation of exactly six or five individuals in twinned orientation. Thus all individuals in a cyclic twin are of the same age.)
The cyclic twinning model, at least as I have presented it, is a contact twinning model. John very appropriately raises the issue that some cyclic twins are interpreted as penetration twins, particularly the standard aragonite twins.
The classic Dana’s Textbook of Mineralogy (author W.E. Ford), and other versions of the Dana series of mineral texts that follow it, distinguish between contact and penetration twinning in one section. They then discuss repeated twinning in another section, distinguishing between repeated twinning with parallel twin planes – polysynthetic twinning, as in the plagioclase feldspars – and repeated twinning with non-parallel twin planes – cyclic twinning if the growth process “goes to completion”. They do not explicitly describe cyclic twinning as a kind of penetration twinning, though examples of cyclic twins by penetration (aragonite) are presented, as are cyclic twins such as marcasite for which the penetration model is inappropriate. Terms like “repeated” or “successive” are frequently used, and tend to imply the “one twin after another” model, though a time sequence is not explicitly stated.
Ford comments that in real crystals the distinction between contact and penetration twinning is often blurred and may not be very important. This may be especially true with cyclic twins.
If we consider an ideal candidate for formation of a flat cyclic twin, let’s say for the moment a twin with a hexagonal outline, it would probably be an orthorhombic or tetragonal mineral with a unit cell that had a prominent crystallographic direction such as {110} where two planes, say (110) and (1-10), made an angle of 60° with each other. Such a mineral, if twinned by contact twinning of six individuals, would produce a perfect hexagonal cyclic twin with no overlap or gap. Similarly, a penetration twin model involving three individuals related by this set of {110} planes, would make a perfect cyclic twin of exactly the same gross morphology.
But unless we knew how this formed or could see detailed evidence that only three crystals were involved, and had crossed each other in the middle like strands of a weaving, we would not know whether it was a penetration twin or contact twin. (And we would not be able to decide whether to call such twins trillings or sixlings.)
2) When, as is the case with most minerals, the relevant set of twin planes do not make a 60° angle, but one of, say, 58° or 65°, the two models lead to different outcomes. Returning for a moment to marcasite, which “wants” to form fivelings with angles between the twin planes of approximately 72°, the contact model leads to very different results than the penetration model, because across from any of the five crystal domains is a region with very different orientation, and a strict penetration model would lead to a crystal with 10 segments!
For minerals that are more nearly commensurate with a 60° twinning model, careful studies of “opposite” crystals might reveal how frequently they are exactly opposite, as a penetration model would suggest they should be, or how often they fail to be opposite by several degrees, which might suggest that a penetration model is inaccurate. In the (unrealistic) sequential contact model, misfit is saved for the last step. In a penetration model of this sort, the misfit is accommodated between adjacent individuals, but opposite individuals should be aligned. In a contact model that involves simultaneous nucleation of all individuals, misfit might occur anyplace, including between opposite individuals.
So a careful of study the angles between all adjacent individuals may help to determine the degree to which contact versus penetration models are correct. In the case of marcasite, perhaps they indicate a perfectly geometric double twin on (101) and (10-1), paired with a simple twin on {110} which approximate a fiveling with two edges of accommodation. In the case of aragonite, we may find that the penetration model is always appropriate.
3) Textbooks often illustrate incomplete cyclic twins, especially of rutile, composed of three or four individuals. To the extent that twinning occurs at nucleation, these are a puzzle, because their shapes are inconsistent with a single point of origin of growth. If completed, they would form a hexagonal donut with a hole in the middle. Illustration of hexagonal cyclic twins generally show a depression in the middle (e.g. the one from Sinkankas in John White's post), but not a real hole.
It is an interesting question, that some may be able to answer, whether such incomplete but repeated twins actually occur, or are just a figment of a crystallographer’s imagination. If they do occur, they would seem to violate the idea that twinning always occurs at the onset of crystal growth, and the question of how they develop their final form is a very interesting one!
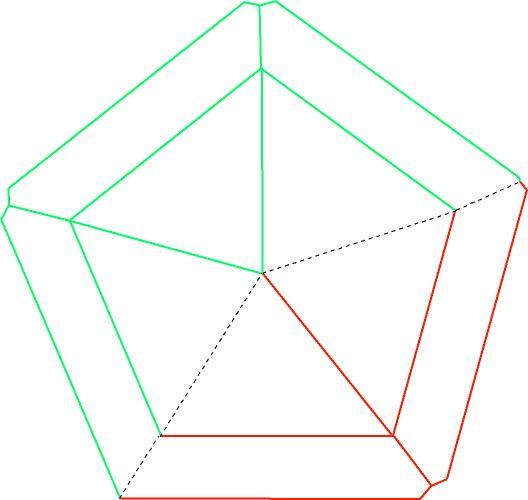
| Description: |
| Aragonite trilling by penetration. The red and green crystals are both twinned to the blue crystal by twinning on {110}. However, the red and green crystals are not twinned to each other. Note that the vertical edges of the trilling are different from the other edges, reflecting the misfit where these two join. |
|
| Viewed: |
74637 Time(s) |
|
| Description: |
| A marcasite fiveling composed of one twin with three individuals, and another with two individuals. The lines where the two twins join are not true twin planes, because the misfit is accommodated there. |
|
| Viewed: |
74631 Time(s) |
|
| Description: |
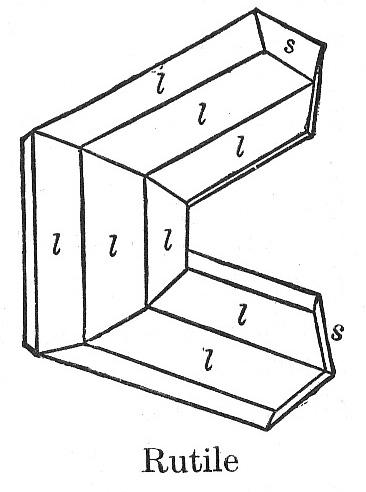
| Rutile double twin, from Dana's Textbook. How did this twin form? |
|
| Viewed: |
74524 Time(s) |
|
_________________
Collecting and studying crystals with interesting habits, twinning, and epitaxy |
|
| Back to top |
|
 |
Pete Richards
Site Admin

Joined: 29 Dec 2008
Posts: 846
Location: Northeast Ohio



|
 Posted: Aug 20, 2012 13:47 Post subject: Re: About cyclic twinning - (5) Posted: Aug 20, 2012 13:47 Post subject: Re: About cyclic twinning - (5) |
|
|
| John S. White wrote: | | Some lillustrations from John Sinkankas' book Mineralogy |
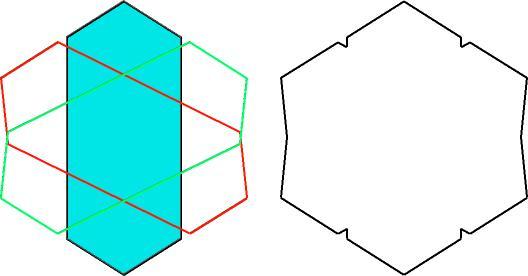
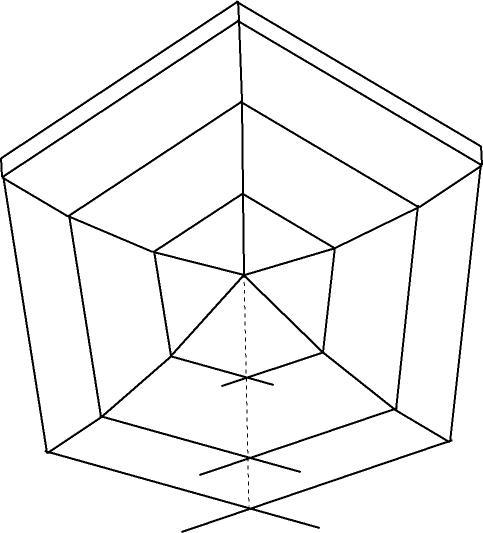
The rutile illustration is often shown, with minor variants (back edges or not, etc). It is interesting that the twin illustrated appears to have a perfect hexagonal outline. But the angle across the twin plane in rutile is 65°, not 60°, so if the crystal is really perfectly hexagonal, there must be 5° of misfit at each twin boundary.
How can nature do this? Or is this our idealization of what really happens?
Here's a cyclic twin of rutile with the individuals all correctly oriented relative to each other....
| Description: |
| Theoretically accurate rutile sixling showing deviation from ideal hexagonal outline. |
|
| Viewed: |
74530 Time(s) |
|
_________________
Collecting and studying crystals with interesting habits, twinning, and epitaxy |
|
| Back to top |
|
 |
Pete Richards
Site Admin

Joined: 29 Dec 2008
Posts: 846
Location: Northeast Ohio



|
 Posted: Aug 20, 2012 13:57 Post subject: Re: About cyclic twinning - (5) Posted: Aug 20, 2012 13:57 Post subject: Re: About cyclic twinning - (5) |
|
|
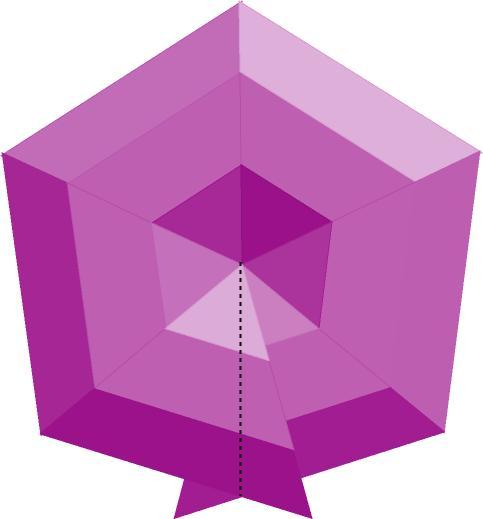
This is perhaps a better version of the drawing, unless you can't stand the purple color. The orientation is more appropriate, and the shading helps reveal the 3-D shape.
| Description: |
|
| Viewed: |
74469 Time(s) |
|
_________________
Collecting and studying crystals with interesting habits, twinning, and epitaxy |
|
| Back to top |
|
 |
Pete Richards
Site Admin

Joined: 29 Dec 2008
Posts: 846
Location: Northeast Ohio



|
 Posted: Aug 20, 2012 14:01 Post subject: Re: About cyclic twinning - (5) Posted: Aug 20, 2012 14:01 Post subject: Re: About cyclic twinning - (5) |
|
|
| Dean Allum wrote: | Pete,
Your competing poly-crystals theory for cyclic twinning is elegant!
Wouldn't there be some remaining evidence of the nucleation site at the central vertex which you could view with a TEM of the thin section?
-Dean Allum |
Thanks!
There might be some evidence of the nucleation site, though the nucleus might be too small to see except with something like TEM. If the crystal is not highly transparent, finding the nucleation site would be quite a challenge - there's no guarantee it would be in the physical center of the twin!
_________________
Collecting and studying crystals with interesting habits, twinning, and epitaxy |
|
| Back to top |
|
 |
mihailovici79

Joined: 07 Sep 2011
Posts: 111
Location: Timisoara



|
 Posted: Aug 20, 2012 14:18 Post subject: Re: About cyclic twinning - (5) Posted: Aug 20, 2012 14:18 Post subject: Re: About cyclic twinning - (5) |
|
|
Is this an example of cyclic twinning?
| Description: |
| Rutile, Semenic Mountains, Romania |
|
| Viewed: |
74381 Time(s) |

|
| Description: |
| Rutile, Semenic Mountains, Romania |
|
| Viewed: |
74448 Time(s) |

|
|
|
| Back to top |
|
 |
|





